1)Периметр правильного треугольника равен 3·√6
Найти площадь части плоскости, расположенной между окружностью, описанной около
треугольника и окружностью, вписанной в этот треугольник.
№2 __
Длина стороны правильного треугольника √54
Около треугольника описана окружность, в эту окружность вписан квадрат. Найти сторону
квадрата.
№3 __
Сторона правильного треугольника равна √24.
В этот треугольник вписана окружность, а в окружность вписан квадрат. Найти сторону
квадрата.
№4 Сторона квадрата равна 6. В этот квадрат вписана окружность, а в окружность вписан
правильный треугольник. Найти сторону треугольника.
№5 У кругового сектора величина угла в радианной мере составляет П/5. Площадь этого
кругового сектора равна 26. Найти площадь круга, частью которого является этот круговой
сектор.
№6 Длина окружности равна 1920П. Найти длину дуги, на которую опирается центральный
угол, величина которого в радианной мере составляет 17П/60
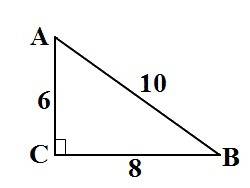
AB - гипотенуза
BC = 8 см - катет
AC - катет
По условию
AB = BC + AC - 4
AB = 8 + AC - 4
AB = AC + 4
По теореме Пифагора:
AB² = BC² + AC²
AB² = 8² + AC²
AB² = AC² + 64
(AC + 4)² = AC² + 64
AC² + 8AC + 16 = AC² + 64
8AC = 64 - 16
8AC = 48
AC = 6 (cм)
Тогда AB = 6 + 4 = 10 (cм)
Получаем прямоугольный треугольник со сторонами 6, 8 и 10.
∠C = 90°
∠A можно определить по синусу угла, т.е. по отношению противолежащего катета BC к гипотенузе AB
sin(A) = BC/AB
sin(A) = 8/10 = 0,8
По таблице Брадиса находим, что данной величине приблизительно соответствует угол 53°7' ≈ 53°
Сумма углов треугольника равна 180° ⇒ ∠B = 180 - 90 - 53 = 37 (°)
∠A является большим из острых углов треугольника ABC.
∠A = 53°
P.S. такой треугольник называется египетским или золотым