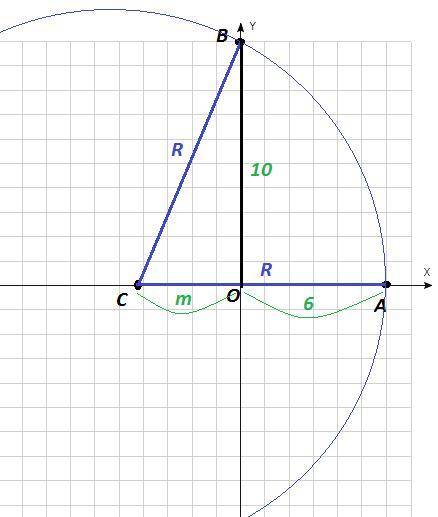
Координаты точки на оси Ox : A (6;0)
Координаты точки на оси Oy : B (0;10)
Так как 6<10, значит, центр окружности лежит слева от оси Oy.
Координаты центра окружности на оси Ox : С(-m;0)
R = CA = m + 6
ΔBOC , R = CB, теорема Пифагора :
R² = m² + 10²
(m + 6)² = m² + 10²
m² + 12m + 36 = m² + 100
12m = 64; 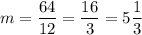
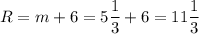
Общее уравнение окружности с центром в точке С и радиусом R
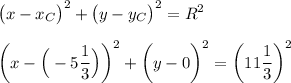
Так как абсцисса центра окружности отрицательная, то в первой скобке должен быть знак плюс.
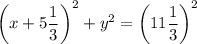
Если подгонять ответ под схему в условии, то знак минус придётся убрать в числитель дроби :
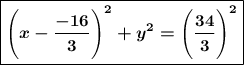
Треугольник АВС правильный, значит точка D лежит ВНЕ треугольника. Значит есть два варианта ответа, для точек D, симметричных относительно Стороны АВ треугольника.
В первом случае <BAD=90°, значит <CAD=30° (90°-60°).
Треугольник АВD равнобедренный (прямоугольный с углами 45°). АВ=АD. Значит треугольник DAC тоже равнобедренный (АС=АD) с углом при вершине 30°. Тогда <ADC=(180-30 ):2=75°, а <CDB=75-45=30°/
ответ: <СDB=30°
Во втором случае:
В равеобедренном треугольнике АD1С (AD1=AC) <D1AC=90+60=150°.
Тогда <AD1C=<D1CA=15°, а <CD1B=45-15=30°
ответ: <СD1B=30°