ответ:√137 (ед. длины)
Объяснение:
Площадь треугольника равна половине произведения высоты на сторону, к которой проведена. Тогда: Ѕ=а•h:2 ⇒ a•h=2S
Высота тупоугольного треугольника, проведенная из вершины острого угла, проходит вне треугольника и пересекает продолжение стороны, к которой проведена.
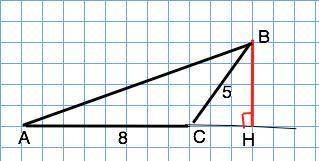
В ∆ АВС проведенная к стороне, равной 8 см, высота ВН=2•16:8=4. Тогда в "египетском" треугольнике ВСН отрезок СН=3 ( то же получим по т.Пифагора).
Треугольник АВН - прямоугольный, АН=8+3=11. По т.Пифагора его третья сторона АВ=√(АН²+BH²)=√(11²+4²)=√137
Объяснение:
По свойству диагонали ромба,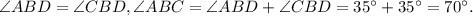
По свойству ромба,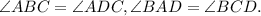
Сумма внутренних углов выпуклого четырёхугольника равна