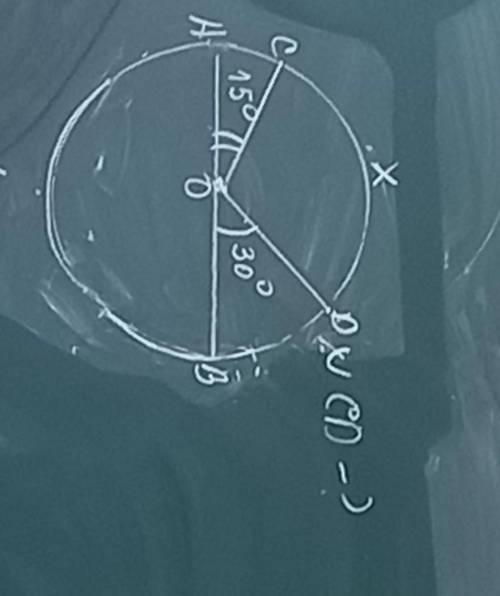
ответ: неверные: 2, 3.
Объяснение: 1 будет правильно по свойству вертикальных углов.
2 будет неверно из-за того, что смежные углы это два угла у которых 1 сторона общая а две другие являются продолжениями одна другой, а на предоставленном примере несказанно то что у них одна сторона общая судя по этому мы можем сказать то что это два любых различных угла.
3 будет неверно из-за того, что вертикальные углы это два угла у которых стороны одного угла являются продолжением сторон другого, а у нас не сказано то что стороны этих углов являются продолжением друг друга, из чего мы можем сделать вывод то, что это неверно.
4 будет верно.
Решение.
По Пифагору найдем второй катет основания призмы:
√(15²-12²)=√(27*3)=9см.
Следовательно, больший катет равен 12см и высота призмы равна 12см (так как боковая грань - квадрат 12х12 - дано).
Площадь боковой поверхности призмы равна Sб=P*h, где Р - периметр, а h - высота призмы.
Sб=36*12=432см².
2) Ребро правильного тетраэдра равно а. Постройте сечение плоскостью, проходящей через ребро АС и делящее его в отношении 1:2, и проходящей параллельно ребру АВ.
Решение.
Условие для однозначного решения не полное.
Во-первых, не понятно условие "Постройте сечение плоскостью, проходящей через ребро АС и делящее его в отношении 1:2".
Проходящее - содержащее это ребро или пересекающее его?
Раз сечение делит ребро в отношении 1:2, значит плоскость пересекает это ребро и делит его в отношении 1:2, но считая от какой вершины?
Во вторых, таких сечений может быть бесконечное множество, так как плоскость, параллельная прямой АВ, может пересекать тетраэдр в любом направлении. Например, параллельно грани АВS (сечение MNP) или проходящее через точку Q на ребре AS (сечение MQDN).
Причем линия пересечения грани АSB и плоскости сечения будет параллельна ребру АВ.
Вывод: однозначного решения по задаче с таким условием нет.