Построение сечения: Назовем искомую плоскость MNK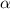 
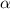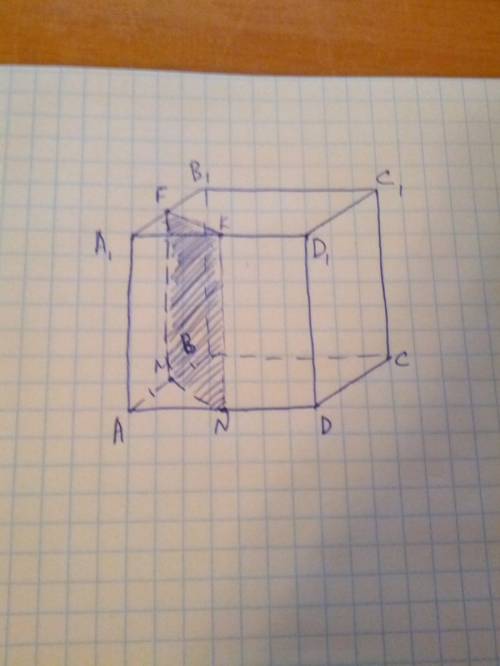
. Плоскости ABC и A1B1C1 параллельны и пересечены плоскостью , следовательно, линии пересечения параллельны. Значит, 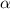пересекает А1В1С1 по прямой КF, параллельной MN. Значит, F - середина А1В1. Осталось соединить KF, FM, MN, NK. Искомое сечение - FKNM.
Доказательство: В треугольнике ABD MN-средняя линия, MN || BD. Т.к MN лежит в плоскости сечения MNK, а BD параллельна прямой MN, лежащей в плоскости сечения, ВD параллельна плоскости MNK, что и требовалось доказать.
Пусть центры окружностей О1 (большей с радиусом R) и О2 (меньшей с радиусом r).
Продлим отрезок О1О2 до точки касания.
Тогда радиус R = 25 + r.
По заданию соотношение R/r = 12/7.
Заменим R: (25 + r)/r = 12/7.Отсюда имеем: 175 + 7r = 12r.
5r = 175
r = 175/5 = 35 см.
Больший радиус равен 25 + 35 = 60 см.
ответ: 60 и 35 см.