
S = 1,125 ед².
Объяснение:
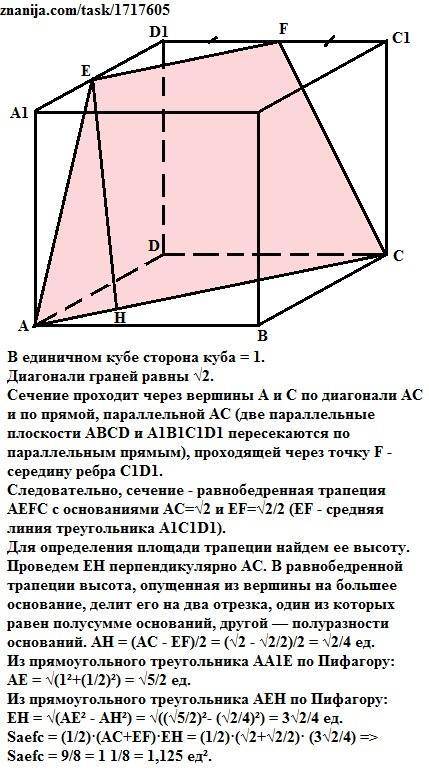
В единичном кубе сторона куба = 1.
Диагонали граней равны √2.
Сечение проходит через вершины А и С по диагонали АС и по прямой, параллельной АС (две параллельные плоскости ABCD и A1B1C1D1 пересекаются по параллельным прямым), проходящей через точку F - середину ребра С1D1.
Следовательно, сечение - равнобедренная трапеция AEFC с основаниями АС=√2 и EF=√2/2 (EF - средняя линия треугольника А1C1D1).
Для определения площади трапеции найдем ее высоту.
Проведем ЕH перпендикулярно АС. В равнобедренной трапеции высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований. АН = (АС - EF)/2 = (√2 - √2/2)/2 = √2/4 ед.
Из прямоугольного треугольника AА1Е по Пифагору:
АЕ = √(1²+(1/2)²) = √5/2 ед.
Из прямоугольного треугольника AЕН по Пифагору:
ЕН = √(АЕ² - АН²) = √((√5/2)²- (√2/4)²) = 3√2/4 ед.
Saefc = (1/2)·(AC+EF)·EH = (1/2)·(√2+√2/2)· (3√2/4) =>
Saefc = 9/8 = 1 1/8 = 1,125 ед².
1. Радиус сферы равен половине диаметра, R = 25 см.
Отрезок, соединяющий центр сферы с центром сечения, перпендикулярен сечению. это и есть расстояние от центра сферы до сечения.
Итак, ОА = 25 см, ОС = 15 см. Из прямоугольного треугольника АОС по теореме Пифагора находим радиус сечения:
АС = √(ОА² - ОС²) = √(25² - 15²) = √(625 - 225) = √400 = 20 cм
Линия пересечения сферы плоскостью - окружность. Ее длина:
C = 2π·AC = 2π · 20 = 40π см
2. Сечение шара - круг. Его площадь равна 36π см²:
Sсеч = π · r² = 36π
r² = 36
r = 6 см
Из прямоугольного треугольника АОС по теореме Пифагора:
ОС = √(ОА² - r²) = √(100 - 36) = √64 = 8 см - искомое расстояние.
3. Радиус большого круга равен радиусу шара.
Площадь сечения:
Sсеч = πr²
Площадь большого круга:
S = πR², R = √(S/π)
Sсеч / S = πr² / (πR²) = r²/ R²
По условию Sсеч / S = 3 / 4, ⇒
r²/ R² = 3 / 4, тогда r/R = √3/2
В прямоугольном треугольнике АОС r/R - это косинус угла А.
Тогда ∠А = 30°.
Расстояние от центра шара до сечения - отрезок ОС. Это катет, лежащий напротив угла в 30°, значит он равен
OC = R/2 = √(S/π) / 2 = √S/(2√π)
4. Радиус шара равен половине диаметра:
R = 2√3 см
Прямоугольный треугольник ОВС равнобедренный, так как в нем острый угол равен 45°, поэтому
ОС = r = R/√2 = 2√3 / √2 = √6 см
Sсеч = πr² = π · (√6)² = 6π см²