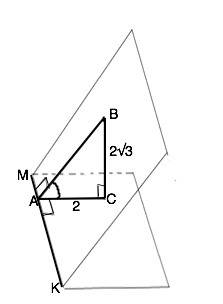
ВС перпендикулярен плоскости, следовательно, перпендикулярен любой прямой, лежащей в этой плоскости и проходящей через его основание С. ⇒ ∆ ВСА - прямоугольный с прямым углом С.
По т.о 3-х перпендикулярах: если наклонная перпендикулярна прямой, лежащей в плоскости, значит, этой прямой перпендикулярна и ее проекция.
ВА - перпендикулярен ребру МК двугранного угла, следовательно его проекция СА перпендикулярна прямой МК.
Величиной двугранного угла является градусная мера его линейного угла.
Линейный угол двугранного угла – угол, сторонами которого являются лучи с общим началом на ребре двугранного угла, которые проведены в его гранях перпендикулярно ребру.
АВ и АС перпендикулярны МК. Следовательно, угол ВАC -искомый.
ctg BAC =2:2√3=1/√3 - это котангенс 60°.
Угол ВАС=60°
Диагональ делит угол пополам - эта диагональ - биссектриса.
Биссектриса трапеции отсекает от нее равнобедренный треугольник. В самом деле:
В треугольнике ВСД угол СВД=углу ВДА как накрестлежащие, угол ВДС=углу ВДА как половины угла АДС. Следовательно, угол ВДС=углу СВД.
ВС=СД.
В трапеции треугольники, образованные диагоналями и основаниями, - подобны. Они имеют по равному вертикальному углу при пересечении биссектрис и равные накрестлежащие углы.
k=AО:ОС=8:6
АД:ВС=8:6
Пусть коэффициент этого отношения равен х
Тогда АД=8х, ВС=6х
Опустим из С высоту СН=12.
АН=ВС, НД=8х-6х=2х, СД=ВС=6х
По т.Пифагора
СД²-НД²=СН²
36х²-4х²=144
32х²=144
х=√4,5=1,5√2 ⇒
ВС=9√2
АД=12√2
S (АВСД)=(21√2)*12:2=126√2 см²