118°, 118°, 62°, 62°
Объяснение:
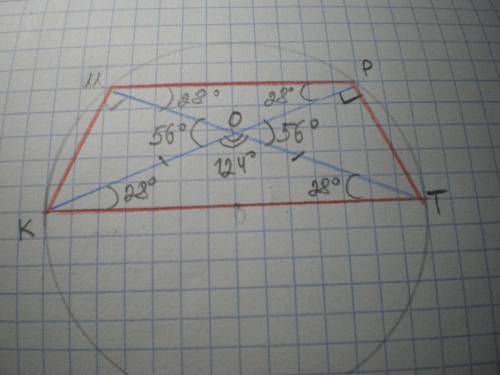
Дано: КМРТ - трапеция, МК=РТ, КТ=D (окружности), КР и МТ - диагонали, ∠РОТ=∠МОК=56°. Найти ∠К, ∠М, ∠Р, ∠Т.
Решение: ΔКМТ=ΔТРК, т.к. КР=МТ как диагонали равнобедренной трапеции, КМ = РТ по условию, сторона КТ - общая. Значит, ∠ОКТ=∠КТО.
∠КОТ=180-56=124°; ∠ОКТ=∠КТО=(180-124):2=28°.
ΔМОР; ∠МРО=∠ОМР=∠ОКТ=∠КТО=28° как внутренние накрест лежащие при МР║КТ и секущих МТ и КР.
∠КМТ=∠КРТ=90° как углы, опирающиеся на диаметр окружности.
∠М=∠Р=90+28=118°
∠К=∠Т=180-118=62° по свойству углов трапеции, прилежащих к боковой стороне
(х-2)²+(у-3)²=4²
(х-2)²+(у-3)²=16
начало координат имеет координаты О(0;0)
(х-0)²+(у-0)²=(5/2)²
x²+y²=25/4 (R=5/2) X²+y²=25 (R=5)
2. C x=(2+4)÷2 y=(7+5)÷2
x=3 y=6
C (3 ; 6) координаты середины отрезка находятся за формулой
х=(х1+х2)÷2; у=(у1+у2)÷2 где (х1; у1) (х2;у2) координаты конца отрезка
АВ ((4-2); (7-5))
АВ (2;2)
АВ²=(4-2)²+(7-5)²=2²+2²=4+4=8
АВ=√8=√4·2=√2²·2=2√2
y=kx+b уравнение прямой если прямая проходит через точки значит ее координаты удовлетворяют уравнение прямой
5=2k+b (×-1) -5=-2k-b
7=4k+b
первое уравнение + второе 2=2k
k=2/2=1
5=2·1+b
b=5-2=3
y=x+3 уравнение прямой которая проходит через точки А и В