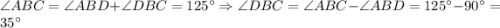Сумма углов треугольника равна 180º, а прямой угол равен 90º, поэтому сумма двух острых углов прямоугольного треугольника равна 90º.Катет прямоугольного треугольника, лежащий против угла в 30º, равен половине гипотенузы.Рассмотрим прямоугольный треугольник ABC, в котором A — прямой, B = 30º и, значит, C = 60º. Докажем, что AC = 1/2 BC. Приложим у треугольнику ABC равный ему треугольник ABD, как показано на рисунке 1. Получим треугольник BCD, в котором B = D = 60º, поэтому DC = BC. Но AC = 1/2 DC. Следовательно, AC = 1/2 BC, что и требовалось доказать.
1)
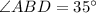; 2)
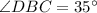
Объяснение:
Рассмотрим два решения (но при этом ответ не поменяется):
Обозначим данный угол буквами
.
Проведём луч
, перпендикулярный лучу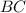 
.
угол, образованный данными лучами с другой стороной угла -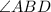
.
Когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.Т.е.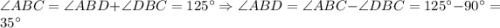
Обозначим данный угол буквами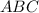
.
Проведём луч
, перпендикулярный лучу 
.
угол, образованный данными лучами с другой стороной угла -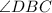
.
Когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.Т.е.