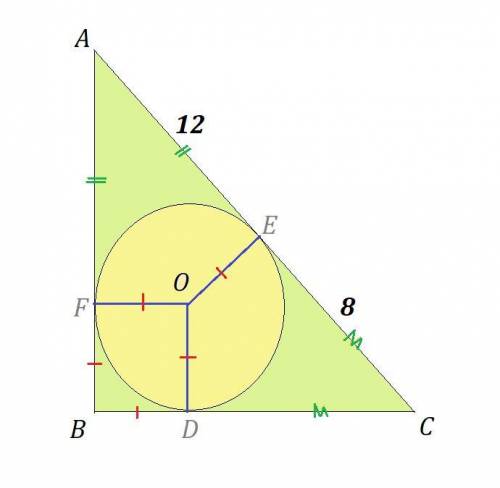
Дано:
ΔABC, ∠B = 90°.
Вписанная окружность с центром O и радиусом OD = OE = OF,
D∈BC, E∈AC, F∈AB.
OE = 12 (см), EC = 8 (см).
Найти:
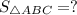
Заметим, что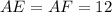 
и 
(так как отрезки касательных, проведенных к окружности из одной точки, равны).
Пусть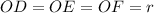 
.
Тогда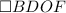 
- квадрат, так как 
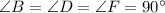(и, значит, 
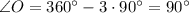), а также 
, 
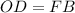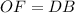и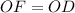 
. - Все стороны и углы данного четырехугольника равны.
Значит,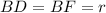 
.
Тогда катеты треугольника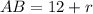 
и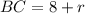 
, а гипотенуза равна 
.
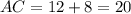По тереме Пифагора:
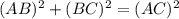
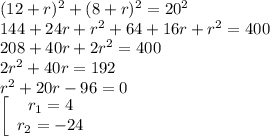
Второй корень нам не подходит (он отрицательный ... ).
Так что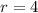 
.
Можем найти площадь:
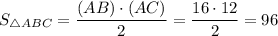
Задача решена!
96 см².
1)описанной
2)вписанным
3)около него
4)описать
5)Г
6)Одну
7)Г
8)В
Объяснение:
Если все вершины многоугольника лежат на окружности, то окружность называется описанной около этого многоугольника, а многоугольник вписанным в эту окружность.
Если сумма противоположных углов четырехугольника равна 180, то около него можно описать окружность.
Около любого треугольника можно описать окружность(вариант г)
Около треугольника можно описать только ОДНУ окружность.
Центром описанной около треугольника окружности является точка пересечения:г
Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:
в)
Теперь рассмотрим треугольник ABL: в нем угол ALB=130градусов(по условию), а угол ABL=34градуса, то угол А = 180-(130+34)=16
Следовательно в треугольнике ABC угол А=16*2 (так как AL биссектриса угла А(BAC)) угол А=32градуса
Теперь найдем последний угол С=180-(32+68)=80градусов
ответ: угол А=32градуса, угол В=68градусов, угол С=80градусов