Формула вычисления длины окружности, зная радиус окружности: 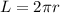
Для начала определим вид треугольника.
Нам уже дано, что около трапеции однозначно описана окружность.
А окружность можно описать только около равнобедренной трапеции!.
Что и означает, что боковые стороны равны — 6; 6.
Другого выбора у нас нет, кроме как объявить, что одно из оснований ровно боковой стороне — 6, а второе основание равно: 12.
Формула вычисления радиусa описанной окружности около равнобёдренной трапеции — такова:
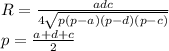
Тоесть, для вычисления этого радиуса — нам должны быть известны основания трапеции, боковая сторона, и! диагональ.
Обозначения сторон: боковые равные стороны равны: "c"; большее основание равно: "b"; меньшее основание равно: "b".
Формула вычисления диагонали равнобедренной трапеции такова: 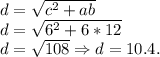
А в этой формуле, переменные таковы: обе боковые стороны обозначаются как "a"; верхнее основание, которое равно боковой стороне — обозначается как "b"; основание с длиной в 12 см — обозначается как "c".
Теперь, зная все стороны трапеции, и диагональ — найдём радиус: 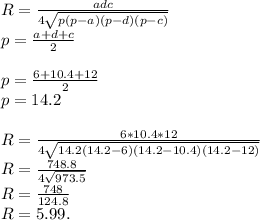
Теперь, зная радиус — найдём длину окружности:

Вывод: L = 37.63.
Треугольники AOD и BOC подобны по свойству трапеции.
Площади подобных треугольников относятся, как квадраты коэффициента их подобия
25:16=k²
k=√(25:16)=5:4
Следовательно, основания трапеции относятся, как 5:4
Обозначим
высоту ᐃ ВОС=h₁
высоту ᐃ АОD=h₂
S АОD=h₂·АD:2
S ВОС=h₁·ВС:2
Площадь трапеции равна произведению ее высоты на полусумму оснований:
Высота трапеции Н
S ABCD=Н·(АD+ВС):2
Н=h₂+h₁
S ABCD =(h₁+h₂)·(АD+ВС):2=
=h₁·АD+h₂·АD+h1·ВС+h₂·ВС
1)
Применим свойство пропорции: произведение средних членов пропорции равно произведению крайних.
h₂:h₁=5:4
4h₂=5h₁
h₂=5h₁/4
S AOD=h₂·АD:2=5h₁/4·АD:2
25=5h₁/4·АD:2 Умножим на два обе части уравнения
12,5=5h₁/4·АD
5h₁/4 =12,5:AD
h₁:4=2,5:AD
h₁·AD= 4·2,5 =10 см²
Т.к. площади боковых треугольников у трапеции равны равны, то h₂·ВС=10 см²
Проверим это:
2)
h₂:h₁=5:4
5h₁=4h₂
h₁=4h₂/5
S ВОС=h₁·ВС:2=4h₂/5·ВС:2
16=4h₂/5·ВС:2 Умножим на два обе части уравнения
8=4h₂/5·ВС
4h₂:5=8:ВС
4h₂·ВС=8·5=40
h₂·ВС=40:4=10 см²
3) Подставим значения h₂·ВС и h₁·AD в уравнение площади трапеции
S ABCD=h₁·АD+25+16+h₂ВС=41+=h₁·АD+h₂·ВС =
S ABCD=10+25+16+10= 61 см