Объяснение:
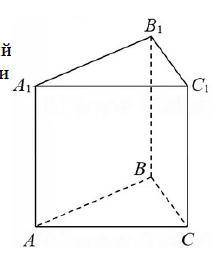
Катет в основании АС=√(13^2-5^2)
АС=√(13-5)(13+5)=√8*18=4*3=12
Р(СС1В1В)=2(ВС+СС1)
2(5+СС1)=40
СС1=15
Sбок=Росн*СС1
Sбок=(13+5+12)*15=30*15=450

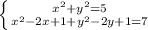
Sполн = 16(12+√3)/3 см².
Объяснение:
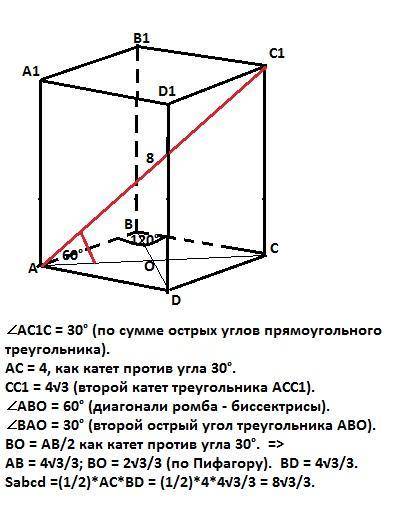
∠АС1С = 30° (по сумме острых углов прямоугольного треугольника).
АС = 4см (катет против угла 30°).
СС1 = 4√3см (второй катет треугольника АС1С).
∠АВО = 60° (диагонали ромба - биссектрисы).
∠АВО = 30° ( второй острый угол - диагонали ромба взаимно перпендикулярны).
ВО = АВ/2 как катет против угла 30°.
АВ = 4√3/3 см; ВО = 2√3/3см (по Пифагору). BD = 4√3/3см.
Sabcd = (1/2)·AC·BD = (1/2)·4·4√3/3 = 8√3/3см².
Sграни = АВ·СС1 = 4√3/3·4√3 = 16см².
S = 2·Sabcd+4·Sграни = 16√3/3 +4·16 = 16(12+√3)/3 см².
450см²
Объяснение:
∆АВС- прямоугольный треугольник
По теореме Пифагора
АВ=√(АС²-ВС²)=√(13²-5²)=√(169-25)=
=√144=12см.
Р(СС1В1В)=2(ВС+СС1)
СС1=Р(СС1В1В)/2-ВС=40/2-5=20-5=15см
Sбок=Росн*СС1
Росн=АВ+ВС+АС=5+13+12=30см
Sбок=30*15=450см²