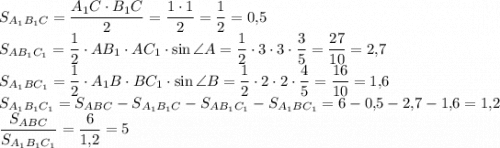Площа прямокутника дорівнює 21 см2 знайдіть сторони Прямокутника Якщо одна з них на 4 см більша Від друго

👇

Открыть все ответы

Ответ:

Chokoladik

12.09.2022

Вся совокупность неровностей земной коры (рельеф)Часть земной поверхности, высоко приподнятая над равниной и сильно расчлененная (горы)Обширные участки с ровной или холмистой поверхностью (равнины)Каменная оболочка Земли, которую образуют земная кора и верхняя часть мантии (литосфера)Равнина, имеющая высоту от 0-200 метров (низменности)Древний, относительно устойчивый участок земной коры, в основании которого лежит древний кристаллический фундамент, покрытый сверху осадочным чехлом (платформа)Равнина, имеющая абсолютную высоту от 500 метров и выше (плоскогорье)Подвижные неустойчивые участки земной коры (складчатость)Равнина, имеющая абсолютную высоту от 200-500 метров (возвышенность)Наука о движение литосферных плит (тектоника)

4,7(25 оценок)

Ответ:

Sykaper

12.09.2022

Объяснение:

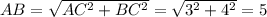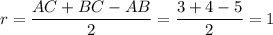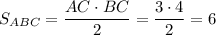Гипотенуза $AB=\sqrt{AC^2+BC^2}=\sqrt{3^2+4^2}=5$ . Радиус вписанной в прямоугольный треугольник окружности $r=\dfrac{AC+BC-AB}{2}=\dfrac{3+4-5}{2}=1$ . Площадь $S_{ABC}=\dfrac{AC\cdot BC}{2}=\dfrac{3\cdot 4}{2}=6$ .

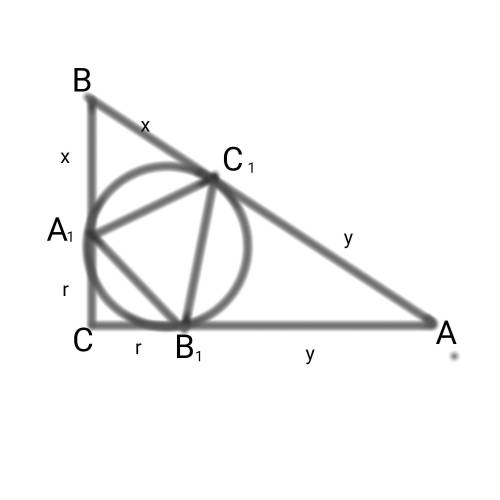
Рассмотрим четырёхугольник OA₁CB₁: ∠С = 90° по условию, ∠A₁ = ∠B₁ = 90° как углы между радиусом и касательной, тогда ∠O = 360° - ∠C - ∠A₁ - ∠B₁ = 360° - 3·90° = 90°. Значит, OA₁CB₁ — прямоугольник, но поскольку OA₁ = OB₁ = r, это квадрат. Тогда OA₁ = OB₁ = B₁C = A₁C = 1.

AC₁ = AB₁ как отрезки касательных, проведённых из одной точки. При этом AB₁ = AC - B₁C = 4 - 1 = 3, т. е. AC₁ = AB₁ = 3. Аналогично BC₁ = A₁B = BC - A₁C = 3 - 1 = 2.

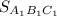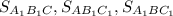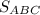Найдём площадь $S_{A_1B_1C_1}$ путём вычитания площадей $S_{A_1B_1C},S_{AB_1C_1},S_{A_1BC_1}$ из площади $S_{ABC}$ :

$S_{A_1B_1C}=\dfrac{A_1C\cdot B_1C}{2}=\dfrac{1\cdot 1}{2}=\dfrac{1}{2}=0{,}5\\S_{AB_1C_1}=\dfrac{1}{2}\cdot AB_1\cdot AC_1\cdot \sin{\angle{A}}=\dfrac{1}{2}\cdot 3\cdot 3\cdot\dfrac{3}{5}=\dfrac{27}{10}=2{,}7\\S_{A_1BC_1}=\dfrac{1}{2}\cdot A_1B\cdot BC_1\cdot\sin{\angle{B}}=\dfrac{1}{2}\cdot 2\cdot 2\cdot \dfrac{4}{5}=\dfrac{16}{10}=1{,}6\\S_{A_1B_1C_1}=S_{ABC}-S_{A_1B_1C}-S_{AB_1C_1}-S_{A_1BC_1}=6-0{,}5-2{,}7-1{,}6=1{,}2\\\dfrac{S_{ABC}}{S_{A_1B_1C_1}}=\dfrac{6}{1{,}2}=5$