В прямой призме ABCA1B1C1 точка K - середина ребра B1C1, AA1:AB:AC = 3:4:5. Найдите угол BAC, если известно, что AK и A1B взаимно перпендикулярны. Варианты: arccos(1/10) arccos(-1/5) arccos(1/5) arccos(-1/10)
Дано:ABC-треугольник. Угол B-30(градусов).(а). Найти:b-?. Решение:Проведем через угол B высоту H.Тогда треугольник ABH-прямоугольный,угол H=90(градусов).Если угол B=30,а H=90,то угол А=60.Угол B=30(градусов)Катет лежащий на против угла в 30 градусов,равен половине гипотенузы.Делим 30:2=15(а).Как же найти b-?.Используем площадь треугольник S=половина * а*b S= половина * 15*b.Видим,что ничего не сокращается,значит умножаем обе части на 2. S=2*половину*15b S=2*15 =30:2=15. 2 ответ:b=15.Если не правильно конечно прости,я сделала,что смогла..
Объяснение:
Определим основания трапеции.
Допустим,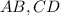
- основания трапеции.
По свойству трапеции,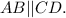
При пересечении двух параллельных прямых секущей, сумма односторонних углов равнаОднако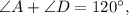
а не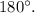 
Значит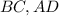
- основания трапеции.
По свойству трапеции,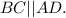
При пересечении двух параллельных прямых секущей, сумма односторонних углов равна