Розв’яжіть прямокутний трикутник АВС, С=90о

,

якщо АС=3см, cos A=1/4

👇

Увидеть ответ

Ответ:

dhgdfnhflk

16.10.2022

Оскільки трикутник прямокутний, то АС = √(АВ² - ВС²) = √(17² - 8²) = 15 см.

cosA = AC/AB = 15/17 ≈ 0,882; ∠A ≈ 28°

cosB = BC/AB = 8/17 ≈ 0,471; ∠B ≈ 62°

Також можна було знайти кут В з властивості гострих кутів прямокутного трикутника: ∠B = 90° - ∠А ≈ 90° - 28° = 62°

Відповідь: АС = 15 см; ∠A ≈ 28°; ∠B ≈ 62°.

Объяснение:

4,5(46 оценок)

Открыть все ответы

Ответ:

kolyapauk2016p08ax4

16.10.2022

Задание 1.
Доказать, что диагонали делят параллелограмм на 4 равновеликих треугольника.
Доказательство.
Диагонали параллелограмма точкой пересечения делятся пополам.
Пусть половина первой диагонали = а, а половина второй диагонали = b.
Значит площадь каждого из получившихся треугольников равна
(1/2)a*b*Sinα - формула, где α - угол между диагоналями.
Углы, образованные при пересечении диагоналей - смежные и равны
α и 180-α.
Поскольку Sin(180-α) = Sinα (формула), то площади всех 4 треугольников равны.
Что и требовалось доказать.
Задание 2.
Найти площадь равнобокой трапеции с основаниями 15 см и 39 см, в которой диагональ перпендикулярна к боковой стороне.
Решение.
Поскольку высота из тупого угла равнобедренной трапеции делит основание на отрезки, меньший из которых равен полуразности оснований = 12см (свойство), а высота нашей трапеции - высота прямоугольного треугольника из прямого угла, то эта высота по ее свойствам равна
h=√((39-12)*12)=18см. Тогда площадь трапеции равна по формуле
S=(AD+BC)*h/2 :
S=(39+15)*18/2=486см².
Задание 3.
Соответствующие стороны двух подобных треугольников относятся как 2 : 3. Площадь второго треугольника равна 81 см2. Найдите площадь первого треугольника.
Площади подобных треугольников относятся как квадрат коэффициента подобия. Значит S1=(2/3)²*S2.
S1=(4/9)*81=36см².
Задание 4.
Основания трапеции относятся как 2:3, а ее площадь равна 50 см2. Найти площади:
а) двух треугольников, на которые данная трапеция делится диагональю
б) четырех треугольников, на которые данная трапеция делится диагоналями.
Решение.
Диагонали трапеции делят ее на 4 треугольника, из которых два, прилежащих к основаниям, подобны, а два прилежащих к боковым сторонам, равновелики (равны по площади).
а). Sabcd=(2x+3x)*h/2 =50см² (площадь трапеции дана). =>
5xh=100см² и xh=20см².
Sabd=Sacd=(1/2)*3xh = 30см².
Sabo=Scod= Sabcd-Sabd= 50-30=20см².
ответ: 30см² и 20см².
б) Sboc=(1/2)*2x*(2/5)h=0,4*xh =0,4*20=8см².
Saod=(1/2)*3x*(3/5)h=0,9*xh =0,9*20=18см².
Saob=Saod=Sabd-Scod=(1/2)*3xh - 0,9*xh = 06xh =12см².
ответ: Sboc=8см²,Saod=18см², Saob=Saod=12см².

4,6(77 оценок)

Ответ:

ketrinkryt

16.10.2022

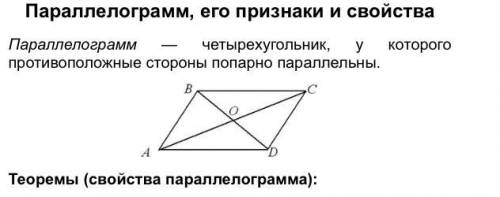
Теоремы (свойства параллелограмма):

В параллелограмме противоположные стороны равны и противоположные углы равны: AB = CD, BC = AD, \angle ABC = \angle

ADC,\angle BAD = \angle BCD.

Диагонали параллелограмма точкой пересечения делятся пополам: AO

= OC, OB = OD.

Углы, прилежащие к любой стороне, в сумме равны 180^\circ .

Диагонали параллелограмма делят его на два равных треугольника.

Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон: AC^2 + BD^2 = 2AB^2 + 2BC^2 .

Признаки параллелограмма:

Если противоположные стороны четырехугольника попарно параллельны, то этот четырехугольник — параллелограмм.

Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.

Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник — параллелограмм.

Если в четырехугольнике диагонали, пересекаясь, точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

Середины сторон произвольного (в том числе невыпуклого или пространственного) четырехугольника K,\;L,\;M,\;N являются вершинами параллелограмма Вариньона.