а) В случае центральной симметрии относительно начала координат, все координаты меняют знак на противоположный:
А (2; 4; 8) - А (-2; -4; -8)
В (4; -3; 10) - В (-4; 3; -10)
С (11; -7; -5) - С (-11; 7; 5)
б) В случае осевой симметрии относительно координатной оси, все координаты, кроме той, которая соответствует данной оси, меняют свой знак на противоположный:
Для оси Ox:
A (2; 4; 8) - A (2; -4; -8)
B (4; -3; 10) - B (4; 3; -10)
C (11; -7; -5) - C (11; 7; 5).
Для оси Оу:
А (2; 4; 8) - А (-2; 4; -8)
В (4; -3; 10) - В (-4; -3; -10)
С (11; -7; -5) - С (-11; -7; 5)
Для оси Оz:
A (2; 4; 8) - A (-2; -4; 8)
B (4; -3; 10) - B (-4; 3; 10)
C (11; -7; -5) - C (-11; 7; -5)
в) В случае зеркальной симметрии относительно координатной плоскости,меняется только та координата, которая не относится к данной плоскости:
Для плоскости хОу:
А (2; 4; 8) - А (2; 4; -8)
В (4; -3; 10) - В (4; -3; -10)
С (11; -7; -5) - С (11; -7; 5)
Для плоскости хОz:
A (2; 4; 8) - A (2; -4; 8)
B (4; -3; 10) - B (4; 3; 10
C (11; -7; -5) - C (11; 7; -5)
Для плоскости уОz:
A (2; 4; 8) - A (-2; 4; 8)
B (4; -3; 10) - B (-4; -3; 10)
C (11; -7; -5) - C (-11; -7; -5)
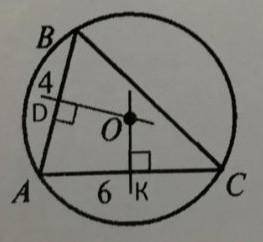
Если из центра окружности (который лежит на гипотенузе) опустить перпендикуляры на катеты, то получится квадрат и два треугольника, подобных исходному. Если обозначить радиус окружности r, больший катет большего треугольника b, меньший катет меньшего треугольника a,
то стороны исходного треугольника будут такие
(a + r, b + r, 35)
стороны меньшего треугольника
(a, r, 15)
стороны большего
(r, b, 20)
и все эти три треугольника подобны между собой.
отсюда a/r = 15/20 = 3/4;
то есть все эти три треугольника - египетские (подобные треугольнику со сторонами 3, 4, 5)
То есть уже можно написать ответ :) вычислять уже ничего не надо, надо просто "подобрать" коэффициенты подобия, чтобы гипотенузы египетских треугольников были бы 15 и 20. Само собой, это 3 и 4.
То есть a = 9, r = 12, b = 16; (получились треугольники 9, 12, 15 и 12, 16, 20)
Исходный треугольник имеет стороны 21, 28, 35, его площадь 294;
длина полуокружности πr = 12π;
Весь "трюк" в том, что r - одновременно больший катет в одном из подобных треугольников и меньший - в другом.