
80°•30°=80•30=2400°
а=2400°
вроде так..
Задание №1
Объяснение:
Пирамида SABCD. Апофема SH - высота треугольника SAB. O - точка пересечения диагоналей основания, SO - высота пирамиды.
1) Рассмотрим прямоугольный треугольник OHS. По теореме пифагора:
OH² = SH² - SO²
OH² = 4a² - 3a²
OH = a
По теореме Фалеса: BC = 2OH = 2a
Сторона основания 2a
2) SHO - линейный угол двугранного угла SABO. Найдя его, найдем и SABO, следовательно угол между боковой гранью и основанием.
Из прямоугольного треугольника SHO:
sin<SHO = SO/SH
sin<SHO = a√3/2a = √3/2
<SHO = 60°
Угол между боковой гранью и основанием 60°
3) S = Sбок + Sосн
В основании квадрат, значит Sосн = AB² = (2a)² = 4a²
Sбок = Pосн*SH/2
Pосн = 4*2a = 8a
Sбок = 8a*2a/2 = 8a²
S = 8a² + 4a² = 12a²
Площадь 12а²
4) Из точки О (это и есть центр основания) проводим перпендикуляр к апофеме SH, обозначаем H1. SH1 - расстояние от центра основания до плоскости боковой грани.
Из прямоугольного треугольника OH1H:
sin<SHO = OH1/OH
но sin<SHO = √3/2
√3/2 = OH1/a
OH1 = a√3/2
ответы: a; 60°; 12а²; a√3/2
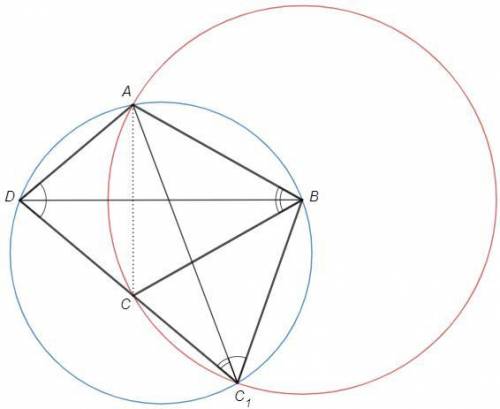
Точки A и С лежат на окружности с центром B.
Стороны угла ADC симметричны относительно биссектрисы DB.
DC пересекает окружность в двух точках (∠DAB не прямой - DA и DC не касательные).
В первом случае точка С симметрична точке A. Тогда DB - биссектриса △ABC, ∠ABC=60, △ABC - равнобедренный с углом 60 - равносторонний, ACB=60°
Во-втором случае (точка C1) докажем, что ABC1D - вписанный.
∠ABD =∠ABC/2 =∪AC/2 =∠AC1D
Отрезок AD виден из точек B и C1 под равным углом - A B C1 D на синей окружности. Тогда ∠AC1B=∠ADB=40°
Объяснение: 30°а : 80°= 110°а