
1)Пусть ABC — данный треугольник (угол C — прямой, AC = 15); CD — высота; BD = 16. Обозначим BD = x. Из подобия треугольников ABC и ACD (угол A общий, ⁄ ADC = ⁄ ACB = 90°) получаем
2)
Пусть а и в катеты треугольника, тогда с=30, т.к. радиус описанной окружности равен половине гипотенузы r=p-c,p=r+c=36, P=36*2=72,a+b=72-30=42.имеем
{а+в=42
a^2+b^2=900
{a^2+b^2=2*ab=42^2=1764
a^2+b^2=900
{900+2*ab=1764
2ab=1764-900
{a+b=42
ab=432
a^2-42a+432=0
а1=18,а2=24
в1=24, в2=18
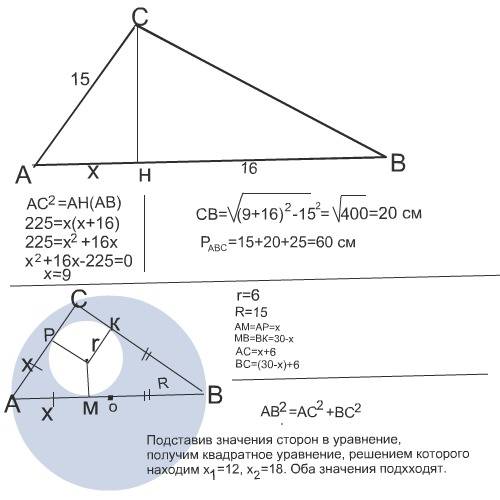
а) Опустим высоту АН из вершины угла, и рассмотрим получившийся прямоугольный треугольник АВН,
{< - угол}
<Н=90°, по определению прямоугольного треугольника, зная сумму всех углов этого треугольника, найдем <ВАН
<ВАН=90°-60°=30°
Против угла в 30° лежит катет равный половине гипотенузы, а значит ВН=0,5*3=1,5
Найдем АН по теореме Пифагора
Найдем НС, зная ВН и ВС,
Рассмотрим треугольник АСН, прямоугольный,
Отсюда,
б) Периметр треугольника равен сумме сторон,
в)Площадь треугольника равна половине произведения АВ на НС и на SinB
или
г) Радиус окружности можно вывести из формулы