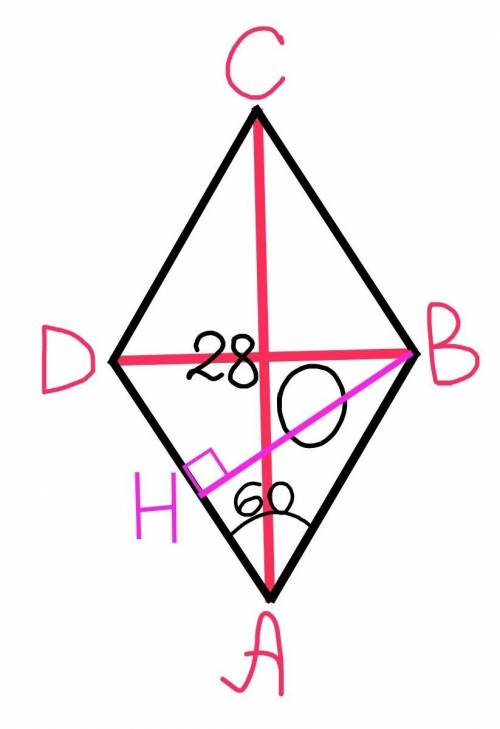
Рассмотрим ∆ВОА и ∆ВНА.
АВ – общая сторона;
Диагонали ромба пересекаясь образуют 4 прямых угла и точкой пересечения делятся пополам.
Следовательно угол АОВ=90°, тоесть ∆ВОА – прямоугольный с прямым углом ВОА, и АО=АС÷2=28÷2=14.
Угол ВНА=90°, так как ВН – высота;
Угол BAD=60° по условию;
Углы при одной стороне ромба в сумме равны 180°.
Тогда угол АВС=180°–угол BAD=180°–60°=120°
Диагонали ромба являются биссектрисами его углов. Исходя из этого: угол DBA=угол АВС÷2=120°÷2=60°
Получим что ∆ВОА=∆ВНА как прямоугольные треугольники с равными острым углом и катетом.
Тогда АО=ВН как соответственные стороны, следовательно ВН=14.
ответ: 14
1. Отрезок FK пересекает прямую РМ
2. При пересечении двух прямых, образуются смежные, а также вертикальные углы. Смежные углы это те, которые на одной прямой, а прямая у нас 180°. Поэтому, мы от 180° отнимаем известный нам угол (58°), находим смежный ему угол (122°). Остальные углы они являются вертикальными по отношению к этим. Поэтому, тот угол, который напротив угла в 58° равен 58°. А тот который напротив 122°,равен 122°.
3. K-середина отрезка CD, то следует что CK и KD равны, а значит 8:2=4см--CK, KD. CM=MK то 4:2=2см--CM,MK. ответ: CM=2cm; MK=2cm; KD=8cm.
Объяснение: