Надо разложить векторы p и q по координатным осям.
Пусть вектор p направлен по оси Ох, вектор q под углом 90 градусов.
Получим координаты: p = (10; 0), q = (0; 1)).
Переходим к векторам a и b.
a =3p + 2q = (3*10 + 2*0 ; 3*0 + 2*1) = (30; 2). Модуль |a| = √904.
b = p - q = (10 - 0; 0 - 1) = (10; -1). Модуль |b| = √101.
Большая диагональ d1 = a + b = (30 + 10; 2 - 1) = (40; 1).
Её длина |d1| = √(40² + 1²) = √1601 ≈ 40,0125
Меньшая диагональ d2 = a - b = (30 - 10; 2 + 1) = (20; 3).
Её длина |d2| = √(20² + 3²) = √409 ≈ 20,224.
Находим угол между диагоналями d1 (40; 1) и d2(20; 3).
По скалярному произведение векторов.
cos A = |40*20 + 1*3|/(√1601*√409) = 803/√654809 ≈ 0,99233.
Угол A = 0,1239 радиан или 7,099 градуса.
Площадь параллелограмма равна модулю векторного произведения векторов a и b или через две диагонали и синус угла между ними.
Находим векторное произведение векторов a(30; 2) и b(10; -1).
i j k | i j
30 2 0 | 30 2
10 -1 0 | 10 -1 = 0i + 0j - 30k - 0j - 0i - 20k = -50.
Площадь по модулю равна 50 кв.ед.
По диагоналям:
S = (1/2)d1d2 sin γ = (1/2)*√1601 * √409 * sin 7,099° = (1/2)*100 = 50 кв.ед.
Задача 6
В ΔАВС , АВ=ВС, АЕ -биссектриса, Е∈ВС. Найти Р( АВС), если ВС-АС=8 и ВЕ:ЕС=3:2.
Решение.
Пусть одна часть х. Тогда ВЕ=3х, ЕС=2х ⇒ ВС=5х ⇒ АВ=5х , т.к треугольник равнобедренный.
По т. о биссектрисе треугольника
, тогда 
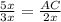⇒ AC=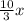
.
По условию ВС-АС=8 , поэтому 5х-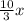
= 8 или 
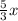=8 или х=4,8.
ВС=5*4,8=24 , АВ=24 , АС=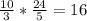
.
Р=24+24+16=64.
Задача 8
Стороны треугольника относятся как 2:3:3 . Найти периметр треугольника , если основание на 5 единиц меньше боковой стороны.
Решение .
Дан ΔАВС. АВ=ВС . Пусть одна часть х. Тогда АВ=ВС=3х, АС=2х .
По условию АС меньше АВ на 5, т.е АВ-АС=5.
Получим 3х-2х=5 или х=5 . Тогда АВ=ВС=3*5=15, АС=2*5=10 .
Р=15+15+10=40.
Задача 9
Угол при вершине равнобедренного треугольника равен 120°. , высота , опущенная на основание, равна 6 .Найти периметр треугольника .
Решение .
Дан ΔАВС , АВ=ВС ,ВН⊥АС , ∠АВС=120°.
1) Высота равнобедренного треугольника является биссектрисой ⇒∠АВН=60° .
2) ΔАВН -прямоугольный , по свойству углов ∠А=90°-60°=30°.
Против угла в 30° , лежит катет равный половине гипотенузы , т.е ВН=1/2*АВ ⇒ АВ=12 ⇒ВС=12, т.к треугольник равнобедренный.
По т. Пифагора АН²=АВ²-ВН² или АН²=12²-6² или АН=√18*6=6√3.
3) Высота равнобедренного ΔАВС является медианой, значит АН=НС=6√3 ⇒АС =12√3.
4)Р=12√3+12+12=24+12√3.