
Без рисунка не обойтись.
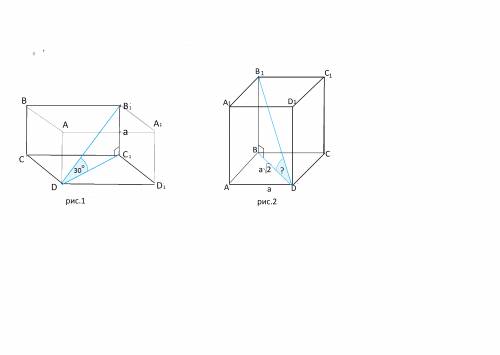
Для наглядности "уложим" призму на боковую сторону (см. рис. 1)
Диагональ В₁D образует с плоскостью DCC₁D₁ угол 30°.
В₁С₁=ВС=а
В₁D=В₁С₁: sin(30 °)=2а
Перейдем к рис. 2.
В₁DВ - угол, образованный диагональю призмы с плоскостью основания.
Стороны угла - диагональ призмы ( она, мы выяснили, равна 2а) и диагональ основания.
Диагональ основания равна, как любая диагональ квадрата, его стороне, умноженной на корень из двух, т.е. а√2
Косинус угла В₁D₁В равен
BD:B₁D=(а√2):2а=√2/2
Это косинус угла 45°.
Так как острый угол прямоугольного треугольника равен 45°, треугольник DВВ₁ равнобедренный.
Отсюда следует равенство высоты призмы и диагонали ее основания.
Высота призмы равна а√2
Биссектриса внутреннего угла треугольника (любого) делит противоположную сторону в отношении, равном отношению двух прилежащих сторон
Рассмотрим треугольник АВС.
ВК - биссектриса и делит АС на отрезки
АК=15 и СК=20.
Отношение этих отрезков 15:20=3:4
Следовательно, АВ:ВС=3:4
Пусть коэффициент отношения сторон будет х.
Тогда АВ:ВС=3х :4х
Коэффициент х найдем по т. Пифагора из треугольника АВС.
АС²=АВ²+СВ²
1225=25х²
х²=49
х=7
АВ=3·7=21
СВ=4·7=28
Биссектриса делит сторону АD на отрезки АЕ и DE
Проведем параллельно АВ из Е прямую ЕМ.
Получили четырехугольник АВМЕ,
в котором ВЕ - его диагональ и биссектриса угла МЕА ( параллельные прямые и секущая ВЕ).
АВМЕ- квадрат со стоной, равной ВА=21
АЕ=АВ=21
DE=28-21=7
ответ: Биссектриса делит сторону прямоугольника на отрезки 21 и 7.