Чертёж смотрите во вложении.
Дано:ΔАВС - прямоугольный.
∠А = 90°.
∠С = 30°.
Точка М - середина СВ.
МН - серединный перпендикуляр.
Доказать:МН < больший катет (АС) в 3 раза.
Доказательство:Сумма острых углов прямоугольного треугольника равна 90°.
Следовательно -
∠С+∠В = 90°
∠В = 90°-∠С
∠В = 90°-30°
∠В = 60°.
Проведём медиану к гипотенузе. Она пересечёт точку М, так как эта точка середина по условию.
Медиана, проведённая к гипотенузе, делит прямоугольный треугольник на два равнобедренных треугольника (так как медиана, проведённая к гипотенузе, равна её половине).
То есть -
ΔАСМ и ΔАМВ - равнобедренные.
Рассмотрим ΔАМВ - равнобедренный. У него есть угол в 60°, а значит, он и равносторонний (признак равностороннего треугольника).
Следовательно, по свойству равностороннего треугольника, ∠АМВ = 60° (каждый угол равностороннего треугольника равен по 60°).
Рассмотрим ΔАСМ - равнобедренный. ∠С = ∠МАС = 30° (так как углы у основания равнобедренного треугольника равны.
Рассмотрим ∠НМВ = 90°.
∠НМВ = ∠НМА+∠АМВ
∠НМА = ∠НМВ-∠АМВ
∠НМА = 90°-60°
∠НМА = 30°.
Так как ∠НМА = ∠НАМ, то ΔАНМ - равнобедренный (по признаку равнобедренного треугольника. Причём НМ = АН (так как лежат против равных углов в одном треугольнике).
Рассмотрим ΔСНМ - прямоугольный. Пусть катет НМ - х.
Против угла в 30° лежит катет, равный половине гипотенузе.
То есть -
СН = 2*НМ
СН = 2х.
Но НМ = АН = х (по выше доказанному).
Поэтому -
АС = СН+АН
АС = 2х+х
АС = 3х.
А теперь составим отношение АС и НМ, и сравним их -
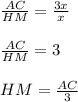
Это нам и нужно было доказать.
ответ:что требовалось доказать.

DOA = 70°. Дано в задаче.
BOC = DOA = 70°. Вертикальные углы равны (1).
DOC = 180° - 70° - 110°. Смежные углы в сумме дают 180° (2).
AOB = DOC = 110°. (1).
ODC = (180° - 110°) / 2 = 35°. Сумма углов треугольника равна 180° (3). Если треугольник равнобедренный, то углы при его основаниях равны (4).
ADO = 90° - 35° = 55°. Два угла составляют прямой угол (5).
OAD = ADO = 55°. (4).
OAB = 90° - 55° = 35°. (5).
OBA = OAB = 35°. (4).
OBC = 90° - 35° = 55°. (5).
OCB = OBC = 55°. (4).
Все остальные углы состоят из других и их можно посчитать по сумме. Например:
DAB = DAO + BAO = 55° + 35° = 90°.