Формула радиуса вписанной окружности
r=S/p, где S- площадь треугольника, р - его полупериемтр
р=(2•10+16):2=36:2=18
Площадь можно найти по ф.Герона, можно, найдя высоту треугольника.
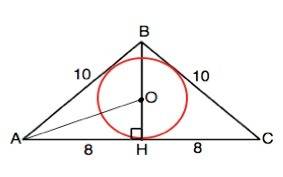
Проведем высоту ВН. Высота равнобедренного треугольника, проведенная к основанию - его медиана и биссектриса.
АН=СН=16:2=8
По т.Пифагора ВН=√(AB²-AH²)=√(100-64)=6
S=BH•AH=6•8=48
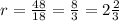
Через свойство биссектрисы решение будет другим.
Центром окружности, вписанной в треугольник, является точка пересечения его биссектрис.
На рисунке приложения ОН=r; BO=6-r
По т.Пифагора найдем ВН=6
Проведем биссектрису АО.
Биссектриса угла треугольника делит противоположную этому углу сторону в отношении, равном отношению двух прилежащих сторон
ОН:ВО=АН:АВ
r:(6-r)=8:10 из пропорции следует
48-8r=10r откуда
18r=48
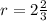
Формула радиуса вписанной окружности
r=S/p, где S- площадь треугольника, р - его полупериемтр
р=(2•10+16):2=36:2=18
Площадь можно найти по ф.Герона, можно, найдя высоту треугольника.
Проведем высоту ВН. Высота равнобедренного треугольника, проведенная к основанию - его медиана и биссектриса.
АН=СН=16:2=8
По т.Пифагора ВН=√(AB²-AH²)=√(100-64)=6
S=BH•AH=6•8=48
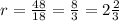
Через свойство биссектрисы решение будет другим.
Центром окружности, вписанной в треугольник, является точка пересечения его биссектрис.
На рисунке приложения ОН=r; BO=6-r
По т.Пифагора найдем ВН=6
Проведем биссектрису АО.
Биссектриса угла треугольника делит противоположную этому углу сторону в отношении, равном отношению двух прилежащих сторон
ОН:ВО=АН:АВ
r:(6-r)=8:10 из пропорции следует
48-8r=10r откуда
18r=48
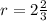

АС = 7 см.
Объяснение:У трикутнику АВС кут С тупий, значить висота ВК опуститься на продовження боку АС за вершину С.
Тоді в прямокутному трикутнику АКВ за Піфагором:
АК = √ (АВ² - ВК²) = √ (20² - 12²) = 16 см.
У прямокутному трикутнику ВКВ за Піфагором:
СК = √ (ВС² - ВК²) = √ (15² - 12²) = 9 см.
АС = АК - СК = 16 - 9 = 7см.