Впрямоугольном треугольнике из вершины прямого угла опущена высота и проведена биссектрисса. расстояние между точками их пересечения с гипотенузой составляет 3 см. найдите площадь треугольника, если расстояние от точки н до одного конца гипотенузы в 4 раза больше расстояния от точки н до другого конца гипотенузы, а точка н - это пересечение гипотенузы и проведенной высоты. заранее всем .
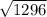 =36
=36
Из подобия треугольников ВСН и АСВ имеем
Пусть СК биссектриса. Т к ВН больший отрезок гипотенузы, то точка К лежит на ВН. По свойству биссектрисы
Получаем равенство
AH=4,5; BH=18.
Из подобия треугольников АСН и СВН имеем
ответ 101,25 кв см