S = 544 ед²
Объяснение:
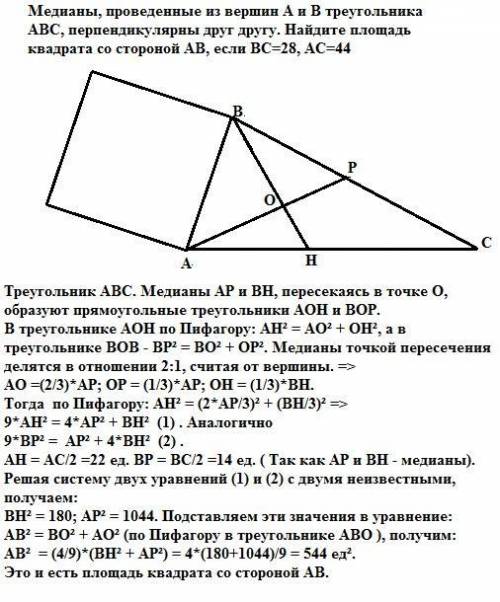
Треугольник АВС. Медианы АР и ВН, пересекаясь в точке О, образуют прямоугольные треугольники АОН и ВОР.
В треугольнике АОН по Пифагору: АН² = АО² + ОН², а в треугольнике ВОВ - ВР² = ВО² + ОР².
Медианы точкой пересечения делятся в отношении 2:1, считая от вершины. =>
АО =(2/3)*АР; ОР = (1/3)*АР; ОН = (1/3)*ВН.
Тогда по Пифагору: АН² = (2*АР/3)² + (ВН/3)² =>
9*АН² = 4*АР² + ВН² (1) . Аналогично
9*ВР² = АР² + 4*ВН² (2) .
АН = АС/2 =22 ед. ВР = ВС/2 =14 ед. ( Так как АР и ВН - медианы).
Решая систему двух уравнений (1) и (2) с двумя неизвестными, получаем:
ВН² = 180; АР² = 1044. Подставляем эти значения в уравнение: АВ² = ВО² + АО² (по Пифагору в треугольнике АВО ), получим:
АВ² = (4/9)*(ВН² + АР²) = 4*(180+1044)/9 = 544 ед².
Это и есть площадь квадрата со стороной АВ.
Расстояние от точки М до середины стороны квадрата (апофема пирамиды МАВСD) ≈ 11 см
Объяснение:
Дано:
Квадрат АВСD
MA = МВ = МС = MD = 12 см
α = 60°
MАВСD - правильная четырёхугольная пирамида
Найти:
Апофему А пирамиды
Опустим перпендикуляр из точки М на основание АВСD. Он пересечёт основание в точке О. МО - высота пирамиды. ОА - проекция бокового ребра МА пирамиды на основание, поэтому заданный в условии угол α = 60° - угол между боковым ребром МА и его проекцией ОА.
В прямоугольном треугольнике МАО (∠МОА = 90°) найдём катеты ОА и МО
МО = МА · sin α = 12 · sin α = 12 · 0,5√3 = 6√3 (см)
OA = MA · cos α = 12 · cos 60° = 12 · 0.5 = 6 (см)
ОА является половиной диагонали квадрата АВСD.
Сторона квадрата а = 2АО : √2 = 12 : √2 = 6√2 (cм)
Апофему пирамиды найдём, используя теорему Пифагора
А² = МО² + (0,5а)² = (6√3)² + (0,5 · 6√2)² = 108 + 18 = 126 (cм²)
А ≈ 11,22 см