Объяснение:
Свойства правильного (равностороннего) треугольника: "В равностороннем треугольнике все углы равны между собой и равны 60°. В равностороннем треугольнике высоты являются и медианами, и биссектрисами. В равностороннем треугольнике точки пересечения высот, биссектрис, медиан и серединных перпендикуляров совпадают. Точка пересечения серединных перпендикуляров - центр описанной окружности.
Определение: "Центроид треугольника (также барицентр треугольника и центр тяжести треугольника) — точка пересечения медиан в треугольнике".
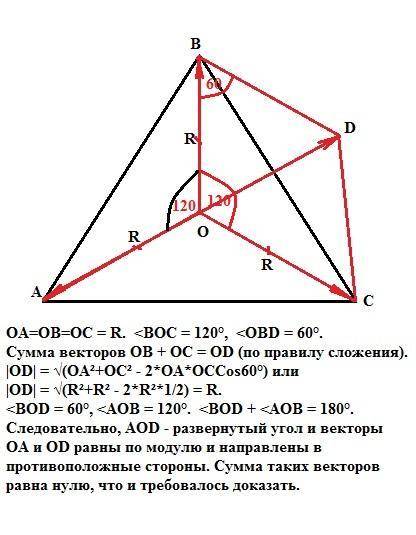
Следовательно, векторы ОА, ОВ и ОС - радиусы описанной около правильного треугольника окружности.
ОА=ОВ=ОС = R.
Сумма векторов ОВ + ОС = OD (по правилу сложения).
<BOC = 120°, <OBD = 60°.
|OD| = √(OA²+OC² - 2*OA*OCCos60°) или
|OD| = √(R²+R² - 2*R²*1/2) = R.
<BOD = 60°, <AOB = 120°. <BOD + <AOB = 180°.
Следовательно, AOD - развернутый угол, векторы ОА и OD равны по модулю и направлены в противоположные стороны. Сумма таких векторов равна нулю, значит сумма векторов ОА+ОВ+ОС = 0, что и требовалось доказать.
Объяснение:
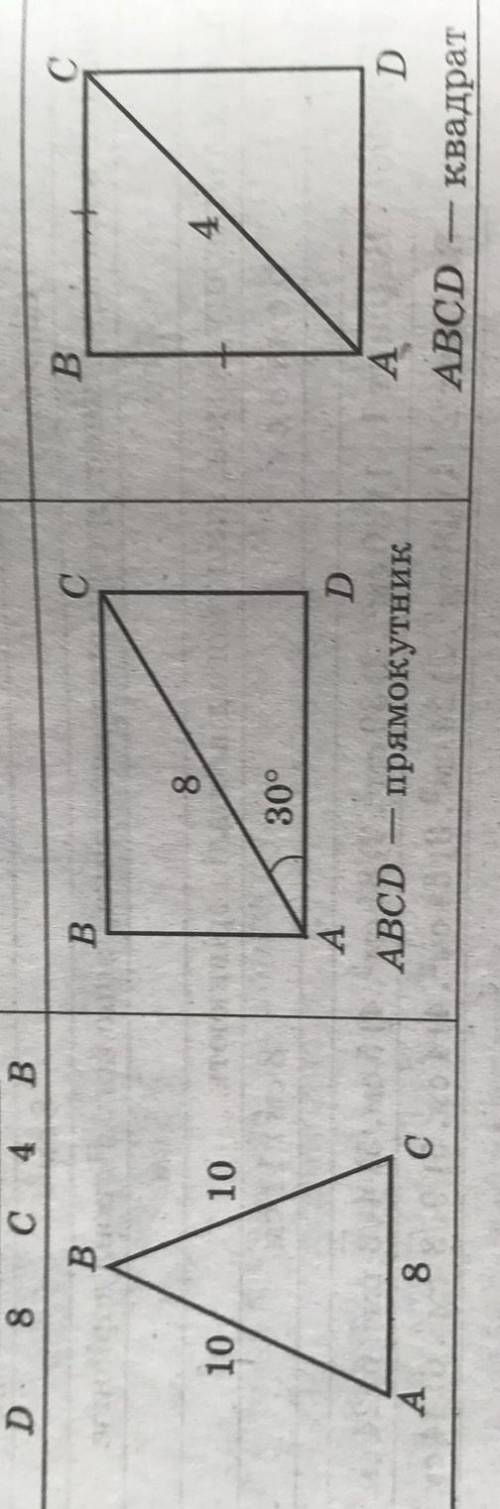
1. Проведем высоту BH. Так как треугольник равнобедренный, то высота является медианой, и AH = CH = AC / 2 = 8/2 = 4
По теореме Пифагора для ΔABH
BH = √(AB^2 - AH^2) = √(10^2 - 4^2 ) = √(100 - 16) = √84 = 2√21
S(ΔABC) = AC*BH/2 = 8*2√21 = 16√21/2 = 8√21
2. <BAD = 90°
<BAC = <BAD - <CAD = 90° - 30° = 60°
AB = AC*cos<BAC = 8*cos 60° = 8 * (1/2) = 4
BC = AC*sin<BAC =8*(√3/2) = 4√3
S(ΔABC) = Ab*BC/2 = 4*4√3/2 = 16√3/2 = 8√3
3. см рис