ВР/РЕ = 15/2.
Объяснение:
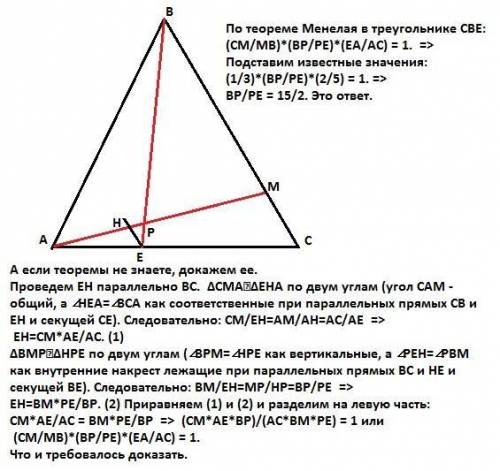
По теореме Менелая в треугольнике СВЕ:
(СМ/МВ)*(ВР/РЕ)*(ЕА/АС) = 1. =>
Подставим известные значения:
(1/3)*(ВР/РЕ)*(2/5) = 1. =>
ВР/РЕ = 15/2. Это ответ.
А если теоремы не знаете, докажем ее.
Проведем ЕН параллельно ВС.
ΔСМА∼ΔЕНА по двум углам (угол CАМ — общий, а ∠НЕА=∠ВСА как соответственные при параллельных прямых СВ и ЕН и секущей СЕ). Следовательно:
СM/ЕН=АM/АН=АС/АЕ =>
ЕН=СM⋅АЕ/AС. (1)
ΔBMP∼ΔHPE по двум углам (∠BPM=∠HPE как вертикальные, а ∠PEH=∠PBM как внутренние накрест лежащие при параллельных прямых BC и HE и секущей BE).
Следовательно:
BM/EH=MP/HP=BP/PE =>
EH=BM⋅PE/BP. (2)
Приравняем (1) и (2) и разделим обе части на левую:
СM⋅АЕ/AС = BM⋅PE/BP => (СM⋅АЕ⋅BP)/(AC⋅BM⋅PE) = 1 или
(СM/МВ)⋅(ВР⋅PЕ)/(ЕA⋅АС) = 1.
Что и требовалось доказать.
АВСД - трапеция , АВ=СД=37 см , ВС=13 см , ВД - биссектриса ∠В .
Так как ВД - биссектриса ∠В , то ∠АВД=∠СВД .
Так как ВС║АД и ВД - секущая, то ∠СВД=∠АДВ как внутренние накрест лежащие углы, и тогда ∠АВД=∠АДВ ⇒ ΔАВД - равнобедренный, АВ=ВД=37 см .
Проведём ВН⊥АД и СМ⊥АД . ВСМН - прямоугольник и МН=ВС=13 см
АН=МД=37-13=24 см , АН=МД=24:2=12 см .
Рассмотрим ΔАВН .
По теореме Пифагора ВН=√(АВ²-АН²)=√(37²-12²)=√1225=35 см .
ВН - высота трапеции.
Площадь трапеции:
S=(АД+BC)/2*ВН=(37+13)/2*35=50/2*35=25*35=875 см²