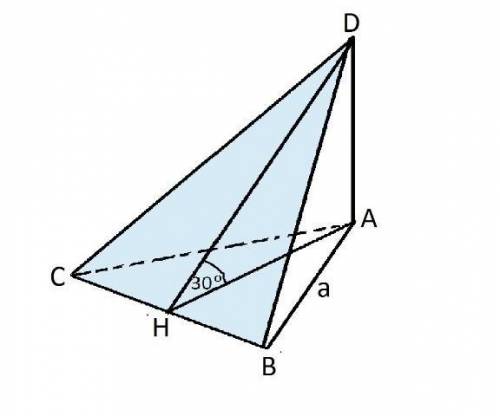
Для решения задачи нужно знать
длину АD, DН и стороны основания,
синус и косинус 30°
АН- высота, медиана и биссектриса треугольника САВ
Треугольник в основании правильный, угол НАВ=60:2=30°
DН=АН:соs 30°
AH=AB*cos 30°=(а√3):2
DН=(а√3):2]:√3):2=а
DА=DН*sin 30°=а/2
Площадь боковой поверхности пирамиды состоит из суммы площадей
треугольника АDВ и 2-х равных треугольников САD и ВАD ( у них равны стороны).
S BDC=DH*CB:2= а*а:2=а²/2
SDAC+S DAB=2*AD*AB:2=2*а²:4=а²/2
Площадь боковой поверхности пирамиды:
S бок =а²/2+а²/2=а²
ответ: Б) (-6;3)
О(0;0)
х1 = х – 6
у1 = у + 3
x1 = -6
y1 = 3
O1(-6;3) Б.