а) Найдем уравнение окружности:
(x-a)²+ (y-b)²=r² (а и b — координаты центра окружности, r – радиус)
r=d/2=8/2=4
Уравнение нашей окружности:
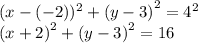
б) Чтобы найти точку пересечения надо подставить уравнение прямой на уравнение окружности вмести y
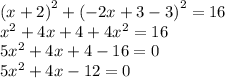
a=5, b=4, c=-12
Найдем по дискриминанту
D=b²-4ac
D=4²-4×5×(-12)=16+240=256
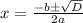
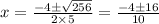
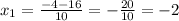
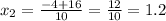
Подставим x в уравнение прямой
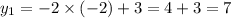
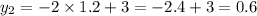
Точки пересечения окружности и прямой
Точки пересечения окружности и прямой(-2 ; 7) и (1,2 ; 0,6)
в) чтобы найти пересечение с осями координат надо приравнять x и y нулю по очереди. Если найти с осью Oy, то надо приравнять x к нулю. А если найти пересечения с осью Ox, то надо приравнять y к нулю.
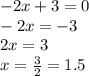
Прямая пересекает ось Ox в точке (1,5 ; 0)
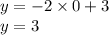
Прямая пересекает ось Oy в точке (0 ; 3)
г)
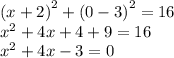
D=16+12=28
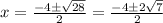
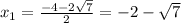
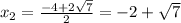
Окружность пересекает ось Ox в точках (-2-√7 ; 0) и (-2+√7 ; 0)
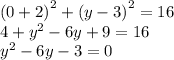
D=36+12=48
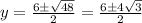
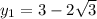
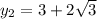
Окружность пересекает ось Oy в точках (0 ; 3-2√3) и (0 ; 3+2√3)
Номер 1
ON-биссектриса треугольника МОК
ЕН-высота треугольника DEC
BP-медиана треугольника АВD
Номер 2
Треугольник равнобедренный по условию задачи,т к РК=РМ
<РНК=90 градусов,т к РЕ-перпендикуляр
<КРН=42:2=21 градус,т к РЕ-биссектриса
Номер 3
Треугольники равны по 2 признаку равенства треугольников-по стороне и двум прилежащим к ней углам
АО=ОD;<BAO=<CDO; по условию задачи
<АОВ=<СОD,как вертикальные
Номер 4
В итоге получились два треугольника,которые равны по 3 признаку равенства треугольников-по трём сторонам
LM=NM;LD=ND; по условию задачи
МD-общая сторона
Равенство треугольников MLD и MND доказано,а это значит,что все соответствующие углы равны между собой
<LMD=<DMN,следовательно,МD-биссектриса угла LMN
Номер 5
При пересечении двух диаметров получились два равных равнобедренных треугольника
МО=ОК;НО=ОР;как радиусы
<МОН=<NOK,как вертикальные
Треугольники равны по 1 признаку равенства треугольников-по двум сторонам и углу между ними
<ОМН=<ОРК=40 градусов
Объяснение: