Рассмотрим ∆ АВD и ∆ СВЕ
Оба прямоугольные и имеют общий острые угол АВС.
Если прямоугольные треугольники имеют равный острый угол, то такие треугольники подобны.
Из подобия следует отношение
ВЕ:ВD=ВС:АВ⇒ВD•ВС=ВЕ•АВ ⇒
ВЕ:ВС=ВD:АВ
Две стороны ∆ ВЕD пропорциональны двум сторонам треугольника АВС, и угол между ними общий.
2-й признак подобия треугольников:
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.
Следовательно, ∆АВС и ∆ ВЕD подобны, что и требовалось доказать.
Можно добавить. что коэффициент подобия равен косинусу общего угла, т.к. отношение катетов ∆ СВЕ и ∆ АВД к их гипотенузам соответственно равны косинусу угла В треугольника АВС.

Дано :
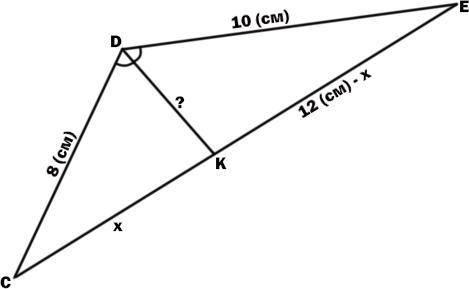
ΔCDE.
СD = 8 см.
DE = 10 см.
СЕ = 12 см.
Отрезок DK - биссектриса ΔCDE.
Найти :
DK = ?
Пусть СК = х, тогда КЕ = 12 (см) - х.
Биссектриса угла треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.Соответственно -
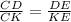
Подставим всё то, что нам известно и находим х -
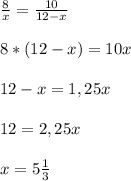
- - -
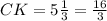 cм
cм
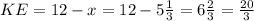 см.
см.
Запишем в виде формулы -
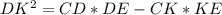
Осталось только подставить и подсчитать -
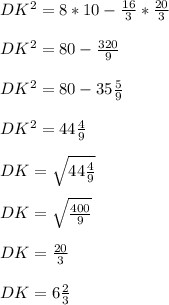
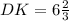 см.
см.
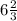 (см).
(см).
ответ: Угол AOD=COB=128 градусов. DOB=AOC=72 градуса