59
Пошаговое объяснение:
59:2=29(ост 1)
59:3=19(ост 2)
59:4=14(ост 3)
59:5=11(ост 4)
59:6=9(ост 5)
Розв'язання.
Випишемо всі двоцифрові числа, які після ділення на 6 дають в остачі 5: 11, 17, 23, 29, 35, 41, 47, 53, 59, 65, 71, 77, 83, 89, 95
Парних та тих, що націло діляться на 3 серед них нема, тому залишається вичеркнути ті, які діляться націло на 5.
Залишилися: 11, 17, 23, 29, 41, 47, 53, 59, 71, 77, 83, 89
З цих чисел, шляхом перевірки, вказані в умові остачі при діленні на 2,3,4,5 дає лише число 59
L1: y = -x-4
L2: y = x-6
Пошаговое объяснение:
Дано:
M(1;-5)
L: 3x+3y+2 = 0
Найти: L1, L2
Решение: 1) Для начала выразим прямую L как каноническое уравнение прямой y = kx+b
3x+3y+2 = 0;
3y = -3x-2|:3;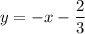
2) Прямые параллельны когда у них меняется свободный член, т.е. k остаётся неизменным, а b нет. Получается коэффициент k у параллельной прямой будет также равен -1
Подставим координаты точки М в каноническое уравнение прямой
-5 = -1*1+b
b = -5+1
b = -4
Уравнение параллельной 3x+3y+2 = 0 прямой, проходящей через точку M(1;-5) будет выглядеть как y = -x-4
3) Для перпендикулярной y = kx+b прямой, проходящей через точку N(x₁,y₁) есть следующая формула:
y-y₁ = -(x-x₁)/k
Получается, перпендикулярная y = -x-²/₃ прямая, проходящая через M(1;-5) будет выглядеть как: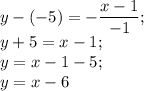
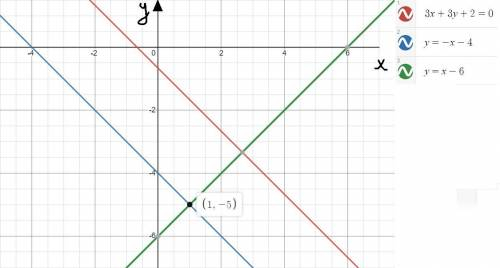
Если построить все данные в одной плоскости, то можно убедиться в правильном нахождении неизвестных прямых(см. вложение)
-2Х=2856
Х= -1428