1
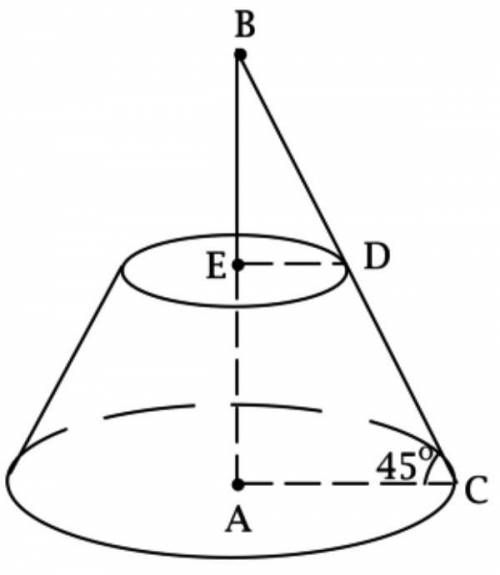
Обозначим центры оснований усечённого конуса через A и E, так что A – центр большего основания. Отметим на большем основании точку C, а точку меньшего основания, через которую проходит образующая, выходящая из C, обозначим через D.
2
Высота AE и образующая CD лежат в одной плоскости. Обозначим точку их пересечения через B. Так как AE – высота, то AE⊥CD и AE⊥AC. Рассмотрим прямоугольный треугольник BAC: в нём ∠BCA=45∘, тогда
3.(первоее фото)
4
Рассмотрим прямоугольный треугольник BED: так как ∠EBD=45∘, то
5.(первое фото)
6
тогда EA=AB−BE=R−r, DC=BC−BD=R2−r2=2(R−r). б о к Sбок=π(R+r)⋅I, где I – образующая, тогда
7(первое фото)

..
Объяснение:
1. ВС=АС-АВ
ВС=7-3=4
2. Треугольник АОВ равен треугольнику СОД по двум сторонам и углу между ними. По первому признаку равенства, который гласит так:
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Отсюда следует, что СД=АВ=6
3. Угол ВСА=угол ВСД:2
Угол ВСА=50°:2=25°. Поделили на два, так как АС-биссеутриса и делит угол на два равных угла.
4. Пусть угол б=70°
Угол б и угол а-смежные. Сумма смежных углов равна 180°.
Угол а=180°-70°=110°
5. Пусть угол 3 равен 145°.
Угол 3 равен углу 2=145°, так как углы вертикальные.
Угол 1 и угол 2-смежные. Сумма смежных углов равна 180°.
Угол 1=180°-145°=35°
6. Одна боковая сторона равна 11. Вторая боковая сторона равна 11, так как боковые стороны равны. Основание равно 4.
Периметр треугольника это сумма всех сторон. Отсюда следует, что:
Р=11+11+4=26
7. Угол С внешний равен внутреннему углу С, так как вертикальные углы. Угол С равен углу А по условию. АС-основание. Мы видим, что углы при основании равны значит треугольник равнобедренный. Одна боковая сторона равна 7. Вторая боковая сторона равна тоже 7. Значит х=7.