Рассмотрим ΔОАД и ΔОСД: у них по условию <ОДА=<ОДС=90, <ОАД=<ОСД, значит и <АОД=<СОД, сторона ОД - общая. Значит эти трегольники равны по стороне и 2 прилежащим к ней углам. Рассмотрим ΔОАВ и ΔОСВ: у них <АОВ=<СОВ (они смежные к равным углам АОД и СОД), сторона ВО - общая и АО=СО (из равенства ΔОАД и ΔОСД). Значит эти треугольники равны по 2 сторонам и углу между ними. Расстояние от точки до прямой - это перпендикуляр, т.е в Δ ОАВ и ΔОСВ это высоты, оущенные из вершины О, опущенные на равные стороны АВ и ВС соответственно. В равных треугольниках равны и высоты, что и требовалось доказать
Если острый угол 60 градусов, то тупой угол будет равен (360-2*60)/2=120 градусовПроведём диагональ из тупого угла. Тупой угол разделиться пополами будет равен 60 градусовПолучим равностронний треугольник. Высота, опущенная из тупого угла будет являться медианой для треугольника, значит сторону разделит на 2 равные отрезка по 20/2=10. есть ромб abcd. из угла b, проведём высоту be, угол abe равен зо градусам т.к угол bed-90 градусов, bcd-60 градусов, cde-120 градусов(180-60), значит отрезок ae равен 20:2=10см(сторона лежащая против угла в 30 градусов, равна половине гипотенузы), ed=20-10=10см. ответ: 10см и 10см Скорее всего так .
длина описаной окружности равна2*пи*R=16 пи, отсюда R=8см
Т.к. треугольник правильный, то R=(a*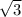
)/3, где а - сторона треугольника, получаем а=24/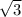
Далее используем формулу для нахождения радиуса вписанной окружности.
r=(a*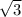
)/6, подставляем а, получаем, что r=4см
длина окружности равна L=2*пи*r=8пи см