Пусть даны две прямые
y=k _{1} xy=k
1
x ,y=k _{2} xy=k
2
x
Причем tg \alpha _{1}=k _{1}tgα
1
=k
1
tg \alpha _{2} =k _{2}tgα
2
=k
2
Найдем тангенс угла между этими прямыми:
tg( \alpha _{1} - \alpha _{2})= \frac{tg \alpha _{1}-tg \alpha _{2} }{1+tg \alpha _{1}tg \alpha _{2} }= \frac{k _{1}-k _{2} }{1+k _{1}k _{2} }tg(α
1
−α
2
)=
1+tgα
1
tgα
2
tgα
1
−tgα
2
=
1+k
1
k
2
k
1
−k
2
Прямые перпендикулярны, угол между ними 90⁰. Тангенс 90⁰ не существует, значит в последней дроби знаменатель равен 0,k _{1} k _{2} =-1k
1
k
2
=−1
это необходимое и достаточное условие перпендикулярности двух прямых
y=k _{1}xy=k
1
x ,y=k _{2} xy=k
2
x
Данная прямая может быть записана в виде y= \frac{5}{2} x+ \frac{7}{2}y=
2
5
x+
2
7
Угловой коэффициент равен 5/2,
Значит угловой коэффициент перпендикулярной ей прямой будет равен (-2/5).
ответ. y=- \frac{2}{5}xy=−
5
2
x
И все прямые ей параллельные, то есть
y=- \frac{2}{5}xy=−
5
2
x +С,
где С- любое действительное число
Объяснение:
решение не мое
ответ: 2√37 см
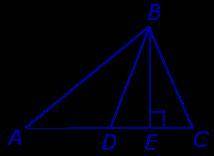
Объяснение: Дано: ΔАВС, АВ=15 см, АС=14 см, ВС=13 см, BD-медиана AD=CD. Найти BD
1) По формуле Герона найдем площадь треугольника
S=√(p(p-a)(p-b)(p-c)) где p-полупериметр
p=13+14+15):2=21
S=√(21(21-13)(21-14)(21-15))=√7056=84
Мы также знаем что S треугольника=1/2а•h возьмем среднюю сторону за основание, проведём высоту h=ВЕ
84=1/2•14• ВЕ ⇒ ВЕ=12 см
2)Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (см рис). ⇒AD=CD=14:2=7 см. На нашем рисунке медианой является отрезок BD.
3) Из прямоугольного ΔВЕС по теореме Пифагора:
CE²=BC²-BE²=13²-12²=169-144=25, ⇒CE=5 см
Тогда DE=CD-CE= 7-5=2 см
4) Из прямоугольного ΔВЕD по теореме Пифагора:
BD²=DE²+BE²=2²+12²=4+144=148 ⇒ BD=√148=2√37 см
Объяснение: осындай щығады