
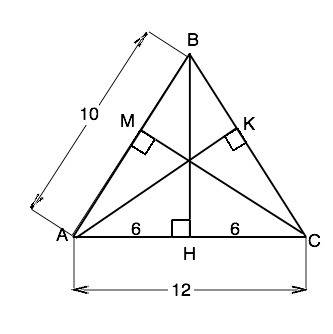
Дан треугольник, две стороны которого равны по 10 см, третья - 12 см. Этот треугольник равнобедренный. Обозначим его АВС, АВ=ВС. Проведем высоту ВН к основанию. Высота равнобедренного треугольника, проведенная к основанию, является его медианой. ⇒ АН=СН=6 см. По т.Пифагора ВН=√(АВ²-АН²)=√(100-36)=8 см. Высоты к боковым сторонам равнобедренного треугольника равны. Найдем их из площади ∆ АВС.
Ѕ(АВС)=АС•ВН:2=48 см² В то же время Ѕ(АВС)=СМ•АВ:2, поэтому СМ•10:2=48 см², откуда СМ=АК=96:10=9,6 см.
Из графика видно, что функция возрастает от (-∞;-2] и от [3;+∞)
Это пока примерное решение, найдём точное
производная функции
f(x) = 2x³ - 3x² - 36x + 11
f'(x) = 3*2x² - 2*3x - 36 = 6x² - 6x - 36 = 6(x² - x - 6)
Найдём нули производной для определения точек экстремумов функции
f'(x) = 0
6(x² - x - 6) = 0
x² - x - 6 = 0
Дискриминант
D = (-1)² - 4*1*(-6) = 1 + 24 = 25 = 5²
Корни
x₁ = (1 - 5)/2 = -2
x₂ = (1 + 5)/2 = 3
Т.е. точки, определённые по графику - точны, и ответ
функция возрастает при
x ∈ (-∞;-2] и x ∈ [3;+∞)