6) Перпендикуляр из центра к хорде делит ее пополам.
(в равнобедренном AOB высота является медианой)
OMC=90 => AM=MB
Радиус в точку касания перпендикулярен касательной.
OHC=90
HOMC - прямоугольник, MC=OH=1
AM=x => AC=4x, MC=3x
AC/MC=4/3 => AC=4/3
9) Диагонали прямоугольника равны, точкой пересечения делятся пополам. Точка пересечения диагоналей прямоугольника равноудалена от вершин и является центром описанной окружности.
Радиус в точку касания перпендикулярен касательной, BDM=90
Сумма острых углов прямоугольного треугольника 90.
MBD =90-50 =40
Вписанный угол равен половине центрального, опирающегося на ту же дугу.
AOD=2ABD =80
10) A=C=70
AOE - равнобедренный (OA=OE, радиусы)
EOC=70+70 =140 (внешний угол)
OEF=90 (радиус в точку касания)
Сумма углов четырехугольника 360
EFC= 360-EOC-OEF-C =360-140-90-70 =60
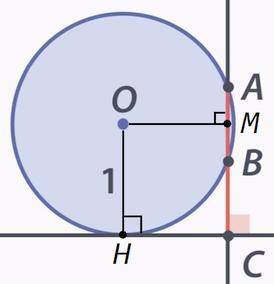
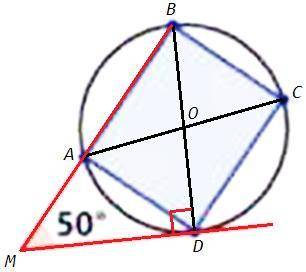

Рисунок надеюсь сам(а) нарисуешь. Решение: АС=АВ так как это касательные проведёные к окружности из одной точки. По свойству о касательных уголСАО=углуВАО. угол АВО= углу АСО=90 градусов. Если АС=АВ, то и АС=12. Тогда, по теореме Пифагора находим гипотенузу, тоесть АО. АО(в квадрате)= ОС (в квадрате) +АС (в квадрате) АО=225(под корнем)=15. ответ 15
либо:
Так как отрезки касательных, проведённых из одной точки к одной окружности, равны, то АВ = АС. Следовательно, АС = 12 см.
Рассмотрим треугольник ОВА: отрезок ОВ равен радиусу окружности, ОВ = 9 см. АВ = 12 см (по условию).
Угол АВО равен 90° (касательная к радиусу проходит под прямым углом). Значит, треугольник ОВА - прямоугольный.
По теореме Пифагора: АО² = AB² + BO² = 12² + 9² = 144 + 81 = 225.
Отсюда АО = √225 = 15 (см).
ответ: АС = 12 см, АО = 15 см.