Объяснение:
Итак, чертеж к задаче прикреплен снизу. Так как треугольник является прямоугольным, то в нем действует теорема Пифагора: квадрат гипотенузы равен сумме квадратов двух катетов прямоугольного треугольника. В алгебраической форме эту теорему записывают так:
c^2 = a^2 + b^2 (^2 - вторая степень числа)
Из этой формулы выразим a^2, т.к. именно катет a нужно найти(см. чертеж внизу)
a^2 = c^2 - b^2
Но мы то выразили только КВАДРАТ стороны, а не саму сторону. То есть, чтобы найти саму сторону, нам нужно извлечь корень квадратный из выражения c^2 - b^2
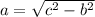
В итоге, вычислив значение а(см. картинку внизу), мы получаем ответ 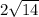

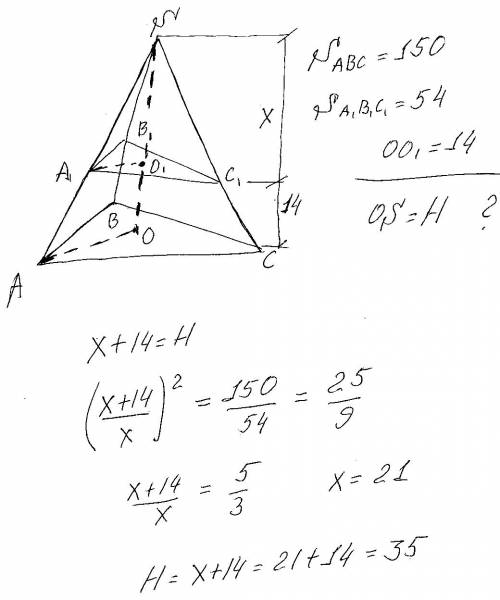
В данном случае не имеет значения что лежит в основании пирамиды-треугольник, квадрат и т.д. При заданных площадях ответ будет одинаковым. Поэтому для простоты нарисуем треугольную пирамиду(смотри рисунок). Треугольники АSС и А1SС1 подобны поскольку АС1 параллельна АС. Следовательно площади треугольников АВС и А1В1С1 относятся как квадраты сходственных сторон А1С1 и АС. Но с тем же коэффициентом подобия в этих треугольниках относятся и стороны А1S и АS. А эти стороны, в свою очередь являются гипотенузами прямоугольных треугольников А1SО1 и АSО(они так же подобны). Следовательно и отношение (ОS/O1S) в квадрате также будет равно отношению указанных площадей, что и приводится в решении(смотри рисунок). ответ Н=35.
56=7*2+2в
56=14+2в
2в=56-14=42
в=42:2=21 см вторая сторона