Задача
Дано:
периметр равностороннего треугольника 18 см
периметр равнобедренного треугольника 20 см
Сторона равностороннего треугольника является основанием равнобедренного треугольника
Найти: стороны равнобедренного треугольника
Решение
1) 18:3=6 (см) - сторона равностороннего треугольника;
2) пусть боковые стороны равнобедренного треугольника равны х см, тогда
х +х + 6 = 20
2х=20-6
2х=14
х=7 (см) - боковые стороны равнобедренного треугольника;
ответ: стороны равнобедренного треугольника равны 6 см, 7 см и 7 см.
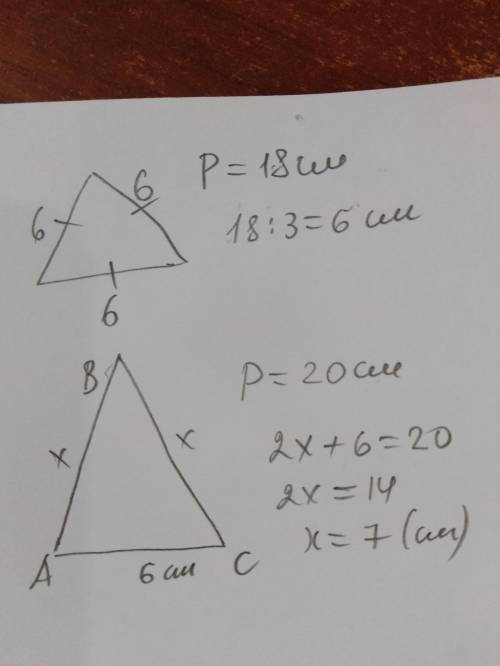
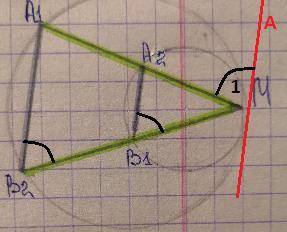
Две окружности касаются внутреннем образом в точке М. Через точку М проведены две прямые, пересекающие одну окружность в точках А₁ , В₂ , а другую в точках А₂, В₁ . Докажите А₁В₂ ║А₂В₁
Объяснение:
Проведем касательную МА . Она является касательной к обеим окружностям .
1) Для малой окружности . Угол ∠1 между касательной МА и хордой А₂М , проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними : ∠1=1/2*∪А₂М
Вписанный угол ∠А₂В₁М=1/2*∪А₂М .Значит ∠1=∠А₂В₁М.
2) Для большей окружности .Угол ∠1 между касательной МА и хордой А₁М , проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними: ∠1=1/2*∪А₁М
Вписанный угол ∠А₁В₂М=1/2*∪А₁М. Значит ∠1=∠А₁В₂М .
3) Т.к. ∠1=∠А₂В₁М , ∠1=∠А₁В₂М ⇒∠А₂В₁М=∠А₁В₂М .
Тогда по признаку параллельности прямых с соответственными углами , при секущей В₂М ⇒ А₁В₂ ║А₂В₁
В сумме углы A + B + C =180 (свойство треугольника). Угол В нам дан, значит мы можем найти сумму двух других:
A+C=180-B
A+C=120.
Нам дано отношение 5 к 7, но это отношение дуг. Значит умножим на 2 сумму углов, чтобы найти сумму длин дуг и разделим на на эти коэффициенты.
5k+7k=120*2
12k=240
k=20
Нам нужно найти угол А, а это половина дуги BC. BC=5k
BC=50*20=100
100\2=50=угол А
Тоже самое с углом С
AB=7k
AB=7*20=140
140\2=70=угол С
Сделаем проверку, <A+<B+<C=180
50+60+70=180. Всё верно
ответ: <A=50, <C=70. <AOC=120