∠B = 30°
Пояснение:
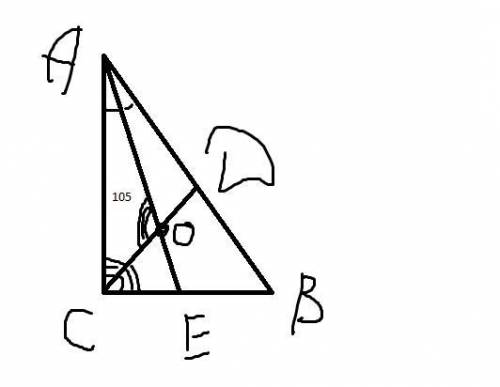
Дано: Δ АВС, ∠С = 90°, ∠АОС = 105°, биссектрисы CD и АЕ, что пересекаются в точке О
Найти: меньший острый угол Δ АВС
Решение
∠CAO = ∠OAD (так как биссетриса AE делит угол ∠А пополам)
∠ACD = ∠OCB= ∠C/2 = 90°/2 = 45° (так как биссетриса CD делит угол ∠C пополам)
Рассмотрим Δ CAO, в котором ∠CAO = 45°, ∠АОС = 105°, ∠CAO - ?
Так как сумма всех углов в треугольнике равна 180°, то
∠CAO = 180° - (105° + 45°) = 180° - 150° = 30°
∠CAO = ∠OAD = 30°, следовательно ∠А = ∠CAO + ∠OAD = 60°
Рассмотрим Δ АВС, в котором ∠С = 90°, ∠А= 60, ∠B - ?
Так как сумма углов при катетах в прямоугольном треугольнике равна 90°, то
∠B = 90° - ∠А = 90° - 60° = 30°
ответ: ∠B = 30°
|а| = 2 см.
Объяснение:
Проведем прямую ВН параллельно СD. Тогда:
Вектор АВ + вектор СD = AB +BH, где вектор ВН = вектору CD.
АВ + ВН = АН (по правилу сложения векторов).
АН = AD - HD (так как НD = BC как противоположные стороны параллелограмма) => AH = 12 - 5 = 7.
Или по теореме косинусов модуль суммы векторов равен:
|AH| = √(AD²-BC²-2·AD·BC·Cos0) = √(25+144-120) = 7.
Вектор AH параллелен вектору ВС, значит
АН - ВС = АР
АР = АН - ВС = 7 - 5 = 2.