
ответ: 5:3
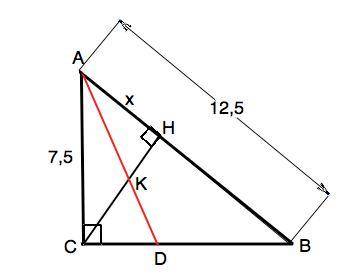
Объяснение: Биссектриса внутреннего угла треугольника делит противолежащую сторону на части, пропорциональные прилежащим сторонам. Обозначим точку пересечения биссектрисы АD и высоты СН буквой К. Тогда СК:КН=АС:АН.
В прямоугольном треугольнике катет есть среднее геометрическое (среднее пропорциональное) между гипотенузой и проекцией этого катета на гипотенузу.
АС - катет, АН его проекция на гипотенузу. Примем АН=х ⇒ АС²=АВ•АН ⇒ 7,5²=12,5•х, откуда х=4,5
Искомое отношение СК:КН=7,5:4,5=5:3
1) Так как треугольник ВАМ (расстояние между В и М соединяем линией) прямоугольный, воспользуемся теоремой Пифагора для нахождения МВ;
МВ²=МА²+АВ²
МВ²=1²+3²
МВ=√10 см
2) ∆МАД также прямоугольный, так что повторяем предыдущие шаги:
МД²=1²+4²
МД=√17 см
(Напоминаю, что длина и расстояние – одно и то же).
3) Диагонали ромба в точке пересечения делятся на двое, так что АД=АС=4 см.
4) По теореме Пифагора ВД²=ВА²+АД²;
ВД²=3²+4²
ВД=√25=5 см
(Диагонали ромба в точке пересечения создают прямой угол).
5) В 3-ем пункте мы нашли отрезок АС, так что теперь приступаем к теореме Пифагора:
МС²=1²+4²
МС=√17 см.
6) Площадь прямоугольного треугольника равна произведению его катетов деленое на два.
Так что S ∆mac = 4×1÷2 = 2 см²