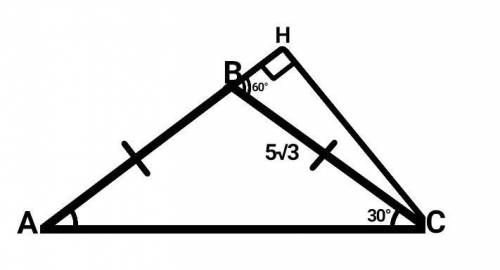
Дано :
∆АВС — равнобедренный (АС — основание).
АВ = ВС = 5√3.
<С = 30°.
СН — высота.
Найти :
СН = ?
В равнобедренном треугольнике углы при основании равны.Следовательно —
<А = <С = 30°.
Внешний угол треугольника равен сумме двух углов, не смежных с ним.То есть —
Внешний <В = <А + <С
Внешний <В = 30° + 30°
Внешний <В = 60°.
Рассмотрим прямоугольный ∆ВСН (СН лежит вне треугольника, так как ∆АВС — тупоугольный).
BC — гипотенуза (так как лежит против угла в 90°).
Тогда —
Sin(<HBC) = CH/BC (по определению синуса острого угла прямоугольного треугольника)
Sin(60°) = CH/(5√3)
Обозначим СН за х.
Тогда —
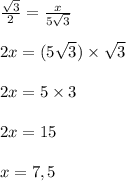
СН = 7,5 (ед).
7,5 (ед).
— — —
Надеюсь, я Вам. Есть вопросы по поводу решения? Задавайте в комментариях.
Объяснение:
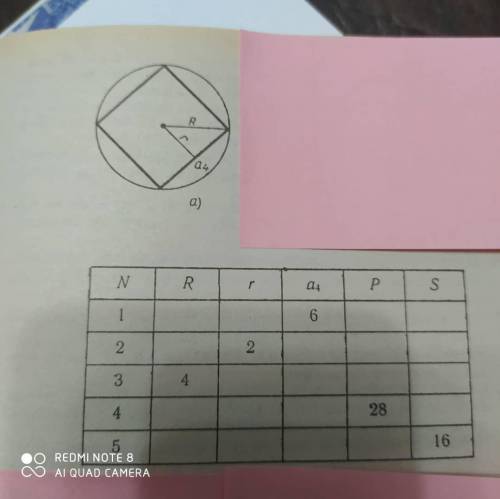
ЗАДАНИЕ 11
На рисунке изображён равнобедренный треугольник, поэтому медиана ZO также является биссектрисой и высотой. На рисунке также показано, что угол Z делится медианой пополам, а также боковые стороны ХZ и ZY равны. По условиям XR=TY, значит RZ= ZT, и RO=TO. Следовательно ∆RZO=∆TZO, а следовательно их углы также равны. Поэтому в ответах верны следующие варианты:
а) RO=TO
г) <ORZ=<OTZ
д) <ROZ=<TOZ
ЗАДАНИЕ 13
Если периметр ∆АВС=36см, а периметр ∆ВСМ=30см, то медина СМ=36–30=6см.
В ∆АВС сумма сторон указана без медианы, а так ∆ВСМ - это половина ∆АВС, при сумме тех же сторон, + ещё и медиана
ОТВЕТ: СМ=6см
ЗАДАНИЕ 14
Рассмотрим ∆СВМ. В нём: ВМ=ВС и СД=ДМ по условиям, поэтому ∆СВМ - равнобедренный и ВД делит сторону СМ пополам, поэтому ВД является медианой и биссектрисой ∆СВМ и <СВД=<МВД. Так как ∆АВС равнобедренный то <А=<В=40°. Угол В является общим для ∆АВС и ∆СВМ. Если <СВД=<МВД=40÷2=20°
ОТВЕТ: <ДВА=20°