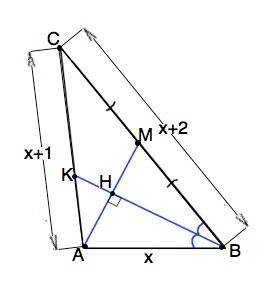
Обозначим медиану АМ, биссектрису ВК.
ВК⊥АМ и пересекает ее в т.Н.
ВН является высотой ∆ АВМ.
Высота и биссектриса совпадают ⇒ треугольник АВМ равнобедренный, ВМ=АВ
Длины сторон треугольника ABC — последовательные целые числа (дано).
Примем сторону АВ=х, АС=х+1, ВС=х+2
Тогда СМ=х+2-х=2
Т.к. АМ медиана, то ВМ=СМ=2, ⇒
ВС=4, АВ=ВМ=2, АС=2+1=3
Предположим, что большей является сторона АС. Тогда АВ=1, ВС=2, АС=3; это противоречит теореме о неравенстве треугольника (3=1+2). Следовательно, АВ=2, АС=3, ВС=4
Периметр АВС=2+3+4=9 (ед. длины)
Угол OBA равен углу OAB и равен 45 градусов.
Значит центральные угол равен 180-(2*45)=90 градусов.
Значит, это прямоугольный треугольник, ещё и равнобедренный.
А в прямоугольном треугольнике медиана (т.к это равнобедренный треугольник, то высота и медиана сходятся) проведённая к гиппотинузе равна её половине половине.
Значит OH =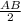 .
.
Значит OH=4 см
ответ: 4 см