
В равнобедренном треугольнике медианы, проведенные к боковым сторонам, равны.
Доказательство: Пусть ABC - равнобедренный треугольник (AC = BC), AK и BL - его медианы. Тогда треугольники AKB и ALB равны по второму признаку равенства треугольников. У них сторона AB общая, стороны AL и BK равны как половины боковых сторон равнобедренного треугольника, а углы LAB и KBA равны как углы при основании равнобедренного треугольника. Так как треугольники равны, их стороны AK и LB равны. Но AK и LB - медианы равнобедренного треугольника, проведённые к его боковым сторонам.
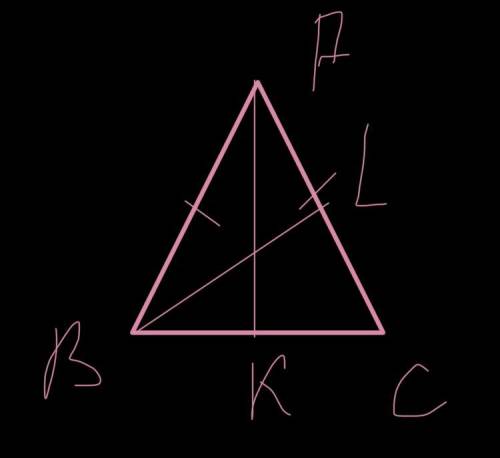
0,8
Объяснение:
1) Косинус - это отношение прилежащего катете к гипотенузе.
2) Прилежащим катетом в данном случае является высота, проведённой к основанию и боковой стороной (в данном случаем гипотенузой).
3) Так как треугольник равнобедренный, то высота ВF, опущенная из вершины В на основание АС, делит это основание на 2 равных отрезка:
АF = FC = 12 : 2 = 6 см.
4) По теореме Пифагора находим высоту BF:
BF^2 = AB^2 - AF^2 = 10^2 - 6^2 = 100 - 36 = 64
BF = √ 64 = 8 см.
5) Находим косинус угла АВF, образованного высотой ВF и боковой стороной АВ:
cos ∠ АВF = ВF : АВ = 8 : 10 = 0,8
ответ: 0,8