Прямоугольник АВСД, угол АСД=60градусов. Рассмотрим треугольник АСД-прямоугольный. Угол САД равен 180-90-60=30градусов. По теореме, катет, лужащий против угла в 30 градусов, равен половине гипотенузы, тогда СД=1 см. По теореме Пифагора АД= см
1. Берем цмркулем гипотенузу и делим ее пополам (надеюсь как делить пополам отрезок с циркуля и линейки не надо рассказывать)
2. Половиной гипотенузы строим окружность.
3. Берем произвольную точку К и проводим через О луч до пересечения с окружностью L. KL будет диаметром и одновременно гипотенузой искомого треугольника.
4. Далее берем циркулем наш катет. Ставим остриё в т.К и делаем засечку на нашей окружности т.М. КМ это наш катет.
Полученный треугольник прямоугольный с искомыми катетом и гипотенузой.
Треугольники AMC и BMC подобны. В подобных треугольниках углы попарно равны. ∠АМС=∠ВМС - по условию. ∠ВСМ≠∠АСМ в противном случае дуга АД была бы равной дуге АД, что в свою очередь ведет к равенству дуг СВД и САД. Из этого получим, что СД - диаметр окружности, перпендикулярный хорде. Тогда получим, что АМ=МВ, что противоречит условию задачи. Значит ∠ВСМ=∠САМ. Составим отношение сходственных сторон в подобных треугольниках. АС/СВ=СМ/МВ=АМ/СМ. В два последних отношения подставим известные данные, получим СМ/9=4/СМ, СМ²=36, СМ=6 Если две хорды окружности, AB и CD пересекаются в точке M, то произведение отрезков одной хорды равно произведению отрезков другой хорды. АМ*МВ=СМ*МВ
Прямоугольник АВСД, угол АСД=60градусов. Рассмотрим треугольник АСД-прямоугольный. Угол САД равен 180-90-60=30градусов. По теореме, катет, лужащий против угла в 30 градусов, равен половине гипотенузы, тогда СД=1 см. По теореме Пифагора АД=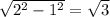 см
см
Площадь прямоугольника равна 1*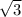 =
=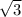 см2
см2
Периметр 2*(1+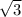 )=2+2
)=2+2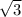 см
см