Дан ромб ABCD; AB=10см; AC+BD=28см.
Найти S(ABCD).
Диагонали ромба перпендикулярны и делятся точкой пересечения пополам. Пусть AC∩BD=O.
AO+BO = AC:2+BD:2 = (AC+BD):2 = 28см:2 = 14см
ΔABO - прямоугольный (∠O=90°). Пусть AO=x см, тогда BO=14-х см
По теореме Пифагора:
AO²+BO² = AB² ⇒ x²+(14-x)²=100²
2x²-28x+96 = 0; x²-14x+48 = 0; x(x-8)-6(x-8) = 0; (x-8)(x-6) = 0
x=6 или x=8
Если AO=6см, то ВО=8см, АС=12см, BD=16см
Если АО=8см, то ВО=6см, АС=16см, BD=12см
Получается ABCD это ромб с диагоналями, равными 16см и 12см.
Площадь ромба равна полупроизведению его диагоналей.
S(ABCD) =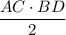 
= 16·12:2 см² = 8·12 см² = 96см²
ответ: 96см².
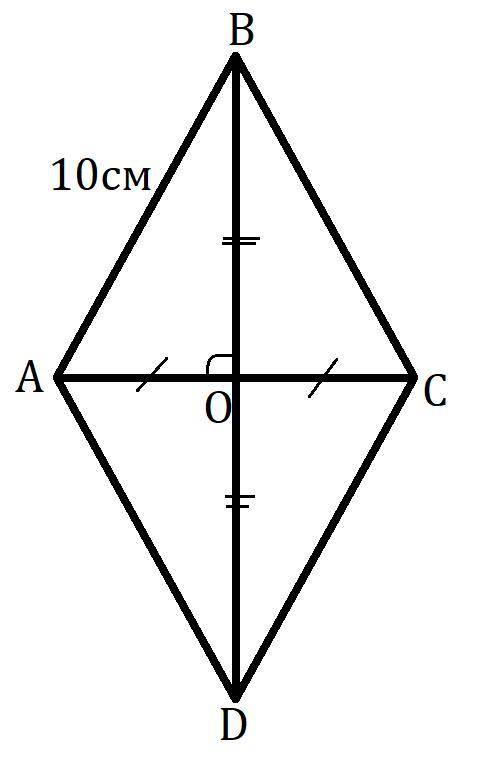
Дан ромб ABCD; AB=10см; AC+BD=28см.
Найти S(ABCD).
Диагонали ромба перпендикулярны и делятся точкой пересечения пополам. Пусть AC∩BD=O.
AO+BO = AC:2+BD:2 = (AC+BD):2 = 28см:2 = 14см
ΔABO - прямоугольный (∠O=90°). Пусть AO=x см, тогда BO=14-х см
По теореме Пифагора:
AO²+BO² = AB² ⇒ x²+(14-x)²=100²
2x²-28x+96 = 0; x²-14x+48 = 0; x(x-8)-6(x-8) = 0; (x-8)(x-6) = 0
x=6 или x=8
Если AO=6см, то ВО=8см, АС=12см, BD=16см
Если АО=8см, то ВО=6см, АС=16см, BD=12см
Получается ABCD это ромб с диагоналями, равными 16см и 12см.
Площадь ромба равна полупроизведению его диагоналей.
S(ABCD) = 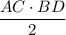= 16·12:2 см² = 8·12 см² = 96см²
ответ: 96см².
Неверно.
Объяснение:
По аксиоме, если две различные плоскости имеют общую точку, то они имеют общую прямую, по которой они пересекаются.
Значит, можно утверждать, что каждая пара из данных трех плоскостей имеет общую прямую.
Но нельзя утверждать, что все три прямые совпадают, т.е. что все три плоскости имеют одну общую прямую.
На рисунке а) точка А общая для трех плоскостей, но общей прямой они не имеют.
На рисунке б) три плоскости имеют общую прямую (но это частный случай)