См. вложение.
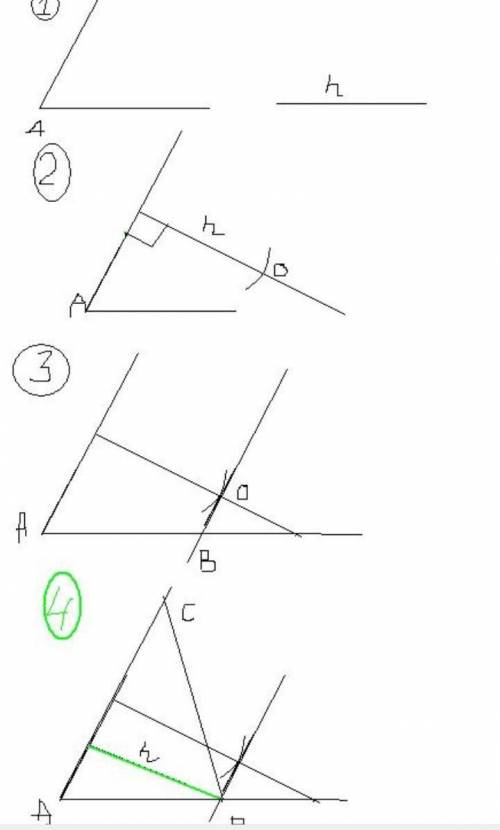
1 дано угол и выстоа
2 Обозначим вершину данного угла буквой А. Строишь перпендикуляр к стороне в любом месте. На перпендикуляре откладываешь высоту. Получилась точка О.
3 Через нее, через точку О то есть, строишь еще один перпендикуляр, чтоб получилась линия параллельная боковой стороне. На ее пересечении с основанием находишь точку В.
4 В точке В строишь заданный угол, только в другую сторону и на пересечении линий находишь точку С. Три точки есть, треугольник построен. Можно проверить длину полученной высоты, показанна зелённым.
1) ΔАВС = ΔABD по первому признаку равенства треугольников:
∠АВС = ∠ABD; AB - общая сторона; ВС = BD.
2) ΔMNK = ΔKPM по первому признаку равенства треугольников:
∠NMK = ∠MKP; MK - общая сторона; MN = KP.
3) ΔАВС = ΔABD по первому признаку равенства треугольников:
∠ROS = ∠POT, как вертикальные; RO = OT; PO = OS.
4) ΔOEF = ΔOMN по второму признаку равенства треугольников:
∠OEF = ∠ABD; ∠EOF = ∠MON; EO = ON.
5) ΔKQM = ΔMFP по второму признаку равенства треугольников:
∠KQM = ∠FPM; ∠QMK = ∠FMP, как вертикальные;
QM = MP.
6) ΔOEF = ΔOMN по второму признаку равенства треугольников:
∠OAC = ∠OCA => OA = OC
∠BOA = ∠DOC, как вертикальные; ∠BAO = ∠DCO;
7) ΔMPE = ΔFPN по второму признаку равенства треугольников:
∠PMN = ∠MNP => MP = PN
∠MPE = ∠NPF, как вертикальные; ∠EMP = ∠PNF;
ΔEMN = ΔMNF по первому признаку равенства треугольников:
∠ЕMN = ∠MNF; EM = FN; MN - общая
8) ΔABC = ΔADC по третьему признаку равенства треугольников:
AB = AD; BC = DC; АС - общая.