1,5 ед.
Объяснение:
Уточненное условие:
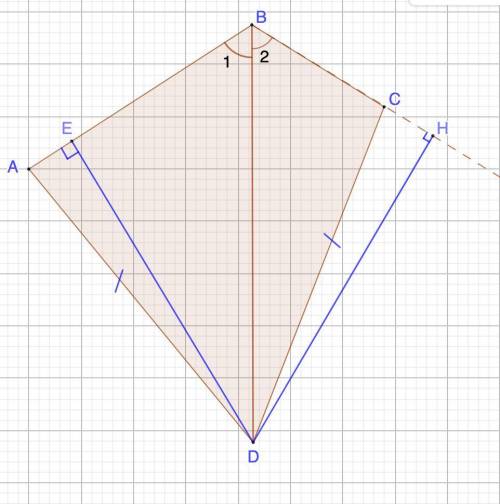
ABCD- выпуклый четырёхугольник, где AВ=7, BC=4,
AD=DC, угол ABD=DBC, точка E на отрезке AB такова, что угол DEB=90°.
Найдите длину отрезка АЕ.
Дано: ABCD- выпуклый четырёхугольник;
AВ=7, BC=4,
AD=DC, ∠ABD=∠DBC, ∠DEB = 90°.
Найти: AE.
Проведем перпендикуляр к продолжению стороны ВС.
1. Рассмотрим ΔDEB и ΔВНD - прямоугольные.
∠1 = ∠2 (условие)
BD - общая.
⇒ ΔDEB = ΔВНD (по гипотенузе и острому углу)
В равных треугольниках соответственные элементы равны.⇒ ЕВ = ВН; ED = HD.
2. Рассмотрим ΔAED и ΔDCH - прямоугольные.
AD = DC (условие)
ED = DH (п.1)
⇒ ΔAED = ΔDCH (по катету и гипотенузе)
АЕ = СН (как соответственные элементы)
3. Пусть АЕ = СН = х
Тогда:
ВН = 4+х
ЕВ = 7-х
ВН = ЕВ (п.1) ⇒
4 + х = 7 - х
2х = 3
х = 1,5
АЕ = 1,5
∠AOB=120° ∠BAM=30°
Объяснение:
ΔАОД=ΔАМД по двум катетам (АД- общий, ОД=ДМ - по условию)
⇒АО=АМ= r
Аналогично из равенства треугольников ВОД и ВМД : ОВ=ВМ= r
Таким образом все стороны четырёхугольник АМВО равны между собой и равны r.
ΔАДМ=ΔВДО - по катету и гипотенузе (ОД=ДМ - по условию, АМ=ОВ=r)
Из равенства треугольников следует равенство сторон: АД=ВД.
Если диагонали четырёхугольника пересекаются и точкой пересечения делятся пополам, то такой четырёхугольник является параллелограммом.
⇒АМВО - параллелограмм. А параллелограмм у которого все стороны равны является ромбом.
Прямоугольный ΔАДО: Катет ОД = 1/2 * ОМ = 1/2* r
Гипотенуза ОА = r
Катет, равный половине гипотенузы, лежит против угла 30 градусов. ⇒∠ОАД=∠ВАМ= 30°
∠ОАМ = 2* ∠ОАД = 2*30°=60°
∠ОАМ и ∠AOB - внутренние односторонние углы при параллельных прямых АМ и ОВ и секущей АО. Их сумма равна 180°
⇒∠AOB=180°-∠ОАМ = 180°-60°=120°

ответ: 10