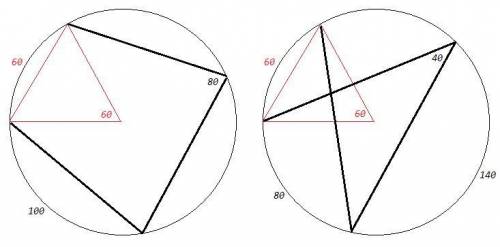
Хорда, равная радиусу, образует с радиусами равносторонний треугольник, следовательно стягивает дугу 60 (центральный угол равен дуге, на которую опирается).
1) Равные звенья стягивают равные дуги (360-60)/3 =100
Дуга между соседними звеньями 100+60=160
Вписанный угол, опирающийся на эту дугу 160/2=80
2) Ломаная может иметь одно самопересечение (очевидно, что соседние звенья не пересекаются, так как уже имеют общую точку). Тогда две дуги имеют общую часть 60 градусов.
Равные звенья стягивают равные дуги (360+60)/3 =140
Дуга между соседними звеньями 140-60=80
Вписанный угол, опирающийся на эту дугу 80/2=40
4) ABCD - вписанный четырехугольник, сумма противолежащих углов 180.
D=180-40=140
5) Углы ABC и AOC опираются на дополнительные дуги, составляющие окружность, 360. Центральный угол (AOC) равен дуге, на которую опирается. Вписанный угол (ABC) равен половине дуги, на которую опирается.
ABC=(360-AOC)/2 =(360-110)/2 =125
6) AOB=360-2ACB =360-100*2 =160
7) Вписанные углы, опирающиеся на одну дугу (или на равные дуги), равны.
ADC =∪AC/2 =ABC =30
8) Вписанный угол, опирающийся на диаметр - прямой, ABD=90.
CBD= CBA+ABD =30+90 =120
9) Диаметр делит окружность пополам, ∪AC=180.
∪AD+∪DC=180 <=> 2ABD+2DAC=180 <=> ABD+DAC=90 <=>
DAC=90-ABD =90-35=55
2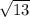 +4, равнобедренный треугольник
+4, равнобедренный треугольник
Объяснение:
Можно решать через вектора:
AB = (2-4, 4-1) = (-2,3) Длина AB = корень из ((-2)*(-2)+3*3) =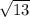
CB = (2-0, 1-4) = (2,-3) Длина CB = корень из (2*2+(-3)*(-3)) =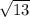
CA = (4-0,1-1) = (4,0) Длина AC =4
Итого: AB = CB, значит треугольник равнобедренный,
периметр = 2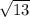 +4
+4
Можно просто через картинку, проведем точку К и найдем CB по теореме Пифагора: CB^2 = KB^2+CK^2 = 2^2+3^2 = 13
Отсюда CB =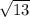
Аналогично AB
CA = 4 из рисунка
периметр = 2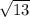 +4
+4