В остроугольном треугольнике ABC из вершин A и C проведена высота AA1 и CC1, причем AA1=CC1. Докажите что треугольник AA1B равен треугольнику CC1B С РИСУНКОМ
Основание правильной четырехугольной призмы- квадрат со стороной а, а=24/4=6 см, боковое ребро ⊥ основанию и равно 10, площадь полной поверхности призмы равна Sбок+2Sосн, Sбок = 10*4а= 10*24=240 см², Sосн= а²= 6²=36 см², Sполн=Sбок+2Sосн=240+2*36= 240+72=312 см², основание правильной треугольной призмы- равносторонний Δ со стороной а=24/3=8 см, и тремя равными углами α= 180°/3=60°, Sосн= а²sin60°/2= (8²*√3/2)/2=64√3/4= 16√3 см², боковое ребро ⊥ основанию и равно 10 см, т е Sбок= 3а*h= 3*8*10=240 см², Sполн= Sбок+2Sосн= 240+ 32√3, сравним площади полных поверхностей этих призм: 312=240+72 > 240+32√3, (√3 < 2) , т е у нас полная поверхность четырехугольной призмы больше треугольной
1. Правильный четырехугольник - квадрат.
Диаметр вписанной в квадрат окружности равен стороне квадрата. ⇒ r=d:2=4:2=2 см.
Для описанного вокруг данной окружности треугольника АВС она - вписанная.
Радиус вписанной в правильный треугольник окружности равен 1/3 его высоты. Следовательно, высота ∆ АВС =2•3=6 см.
Тогда АВ=ВН:sin60°=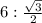 =4√3 см.
=4√3 см.
* * *
2. Для нахождения площади сектора существует формула.
S=Lr:2, где L – длина дуги сектора. ⇒
S=6•4:2=12 см²
Если формула забыта, решить задачу можно без нее.
Длина окружности C=2πr
C=2•p•4=8π см
Площадь окружности S=πr²=16 π см²
Вычислим площадь, которая приходится на сектор с дугой в 1 см.
S:C=16π:8π=2
Тогда площадь сектора
S=2•6=12 см²