Координаты точек A (4; -2), B (1; 2), C (-2; n) и уравнение прямой AB равны 4x + 3y-10 = 0. A) Определите значение n так, чтобы точка C располагалась вдоль линии AB.
Б) Определите, какая из этих точек находится между двумя другими точками.
C) В каком соотношении точка между двумя точками делит отрезок, проведенный через эти точки?
E) Определите координаты точек, соответствующих оси OU, расположенной на 4/5 точки между двумя точками.
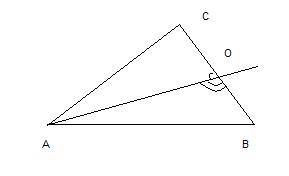
Сумма этих двух углов должна быть равна 180°. Запишем уравнение:
х + (х+20) = 180
2х+20 = 180
2х = 160
х = 80
Итак, <COA = 80°, <BOA = 80+20 = 100°
2. В треугольнике СОА находим угол САО, зная, что сумма углов треугольника равна 180°:
<CAO = 180 - <C - <COA = 180 - 90 - 80 = 10°
3. Поскольку АО - биссектриса, то угол А треугольника АВС равен:
<A = <CAO * 2 = 10 * 2 = 20°
4. Зная угол А и С в АВС, находим неизвестный угол В:
<B = 180 - <C - <A = 180 - 90 - 20 = 70°